Sam

Paramétrage du congé

Démonstration mathématique

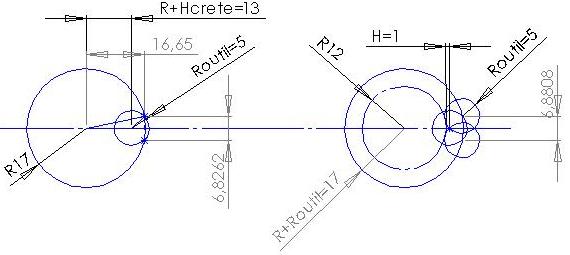
Pour le calcul il faut tout d'abord calculer le pas réel, et la la géométrie n'est pas si simple

On se rend compte que le calcul du pas passe par l'intersection de deux cercles alignés sur y. Nous prendrons deux cercles de rayon R et r
Soit l'équation des deux cercles A et B :$$(x-x_A)^2+(y-y_A)^2=R^2$$ et $$(x-x_B)^2+(y-y_B)^2=r^2$$ Nous pouvons considéré le point A cercle d'origine avec pour coordonnées (0,0) et comme les deux cercles sont alignés alors y_B=0 alors : $$x^2+y^2=R^2,\quad\quad \text{(1)}$$ et $$(x-x_B)^2+y^2=r^2,\quad\quad \text{(2)}$$ Développons (2) $$x^2+x_B^2-2\cdot x \cdot x_B+y^2=r^2$$ regroupon $$(x^2+y^2)+x_B^2-2\cdot x \cdot x_B=r^2$$ Par substitution $$R^2+x_B^2-2\cdot x \cdot x_B=r^2$$ $$R^2+x_B^2-r^2=2\cdot x \cdot x_B$$ $$\dfrac{R^2+x_B^2-r^2}{2\cdot x_B}=x$$

On remplace par les variables d'usinage $$\dfrac{(R+R_{outil})^2+(R+h)^2-R_{outil}^2}{2\cdot (R+h)}=x$$ Donc les coordonnées d'intersection donne : $$x=\dfrac{2\cdot R(R+R_{outil}+h)+h^2}{2\cdot (R+h)}$$ nous avons donc la distance de la médiatrice de contact, et enfin d'après (1) $$y=\sqrt{R^2-x^2}$$ $$y=\sqrt{(R+R_{outil})^2-x^2}$$ la pas donne donc $$pas=2\times \sqrt{(R+R_{outil})^2-x^2}$$

Optimisation enlèvement de copeaux

Pour le calcul il faut tout d'abord calculer le pas réel, et la la géométrie n'est pas si simple

Source d'information catalogue Hoffman-group
Le volume total de copeaux à enlever est $$V=R^2-\dfrac{\pi \cdot R^2}{4}$$ $$V=\dfrac{R^2\cdot(4-\pi)}{4}$$

Programme

N° Programme
Rayon d'outil	N° Outils	Vitesse outils (RPM)	Vitesse avance outils travail (mm/min)
D	R	Hauteur de crête (mm)	Réserve (mm)
Position Z à partir du G54

Clicker sur le type de programme

L'Usinage

Pour le calcul il faut tout d'abord calculer le pas réel, et la la géométrie n'est pas si simple

Pour le calcul il faut tout d'abord calculer le pas réel, et la la géométrie n'est pas si simple