Le Servo-moteur SG90
Caractéristique du Servo-moteur SG90
| Torque | 25.0 oz-in (1.80 kg.cm) at 4.8V |  |
| Speed | 0.1sec/60° (4.8V) | |
| Voltage | 4.0V to 7.2V, 4.6V - 5.2V nominal | |
| Running current with 5V supply (no mechanical load) | 220 ±50mA | |
| Stall current with 5V supply (horn locked) | 650 ±80mA | |
| Idle current with 5V supply | 6 ±10mA | |
| Dimensions | 0.91in x 0.48in x 1.14in (23mm x 12.2mm x 29mm) | |
| Weight | 0.32oz (9g) | |
| Dead band width | 10µs | |
| Operating Temperature range | -22°F to 140°F (-30°C to 60°C) | |
| Universal "S" type connector fits most receivers | ||
Fonctionnement du servo-moteur
|
Contrôler un servo-moteur à l'aide d'un microcontrôleur est simple, aucun pilote externe. Le principe de base est assez simple. Il suffit d'envoyer une impulsion et c'est le temps que durera cette impulsion qui déterminera l'angle du servo-moteur. ce temps d'impulsion est de quelques de quelques millisecondes et doit être répété à intervalle régulier ( 50Hz soit toutes les 20 ms ). Si le temps d'impulsion varie d'un fabricant à l'autre, les valeurs sur ce schéma sont assez standard. |
Programme pour réglage des positions avec le port série
Principe de fonctionnement
Le programme
//Réglage du Servo moteur par position angulaire
//(c) sammy76.free.fr
#include "Servo.h>"
Servo myservo; // Créer l'objet Servo pour contrôler servomoteur
// 9 servomoteurs maximum
int pos = 0; // variable de sauvegarde de positon servo
static void videbuffer_att() {
while (Serial.available() > 0) {
char t = Serial.read();
}
do {} while (!Serial.available());
}
static int readnumber() {
//lit une chaine de caractère et la converti en entier
videbuffer_att();
while (Serial.available() == 0);
int newpos = Serial.parseInt(); //lit int
return newpos;
}
void setup()
{
myservo.attach(9); // Attache le servo à la broche 9 de l'arduino Nano
Serial.begin(9600);
Serial.print("Configuration du Servo 9g\nSaisir la position initiale\n");
}
void loop()
{
pos = readnumber();
/*if (pos<10){
pos=10;
}*/
myservo.write(pos);
Serial.print("Position : ");Serial.println(pos);
delay(1000); // wait for one seconds
}
Dimensions du servo-moteur

Contrôle de servomoteurs avec Microcontrôleurs AVR type Attiny45.
Vous pouvez utiliser la fonction micro-contrôleurs PWM AVR pour contrôler des servomoteurs.Le module Timer/Counter0 qui est une minuterie sur 8bits et dispose de deux canaux PWM (A et B). La fréquence du processeur est 8MHz
De cette façon, le PWM avec génération automatiquement des signaux pour s'occuper des servomoteurs et le micro-contrôleurs est libre de faire d'autres tâches.
Recherche de la valeur de TOP
Avec un choix entre 9 ; 64 ; 256 ; 1024, j'ai choisi le pré-diviseur par 64. Donc, la minuterie se 8MHz / 64 = 125kHz (soit des périodes de 8μS).$F_{pwm}=\dfrac{F_{cpu}}{N(1+TOP)}$ avec $F_{pwm}$ la fréquence du PWM ; $F_{cpu}$ fréquence du CPU (ici 8MHz) ; $N$ prédiviseur (ici 64)
$TOP=\dfrac{F_{cpu}}{F_{pwm}\cdot N}-1$
$TOP=\dfrac{8~000~000~Hz}{50~Hz\times 64}-1=2499$
FREQUENCY = ((CLOCK-SPEED/PRE-SCALER)/256)
Modifier un micro-servomoteur (SG90) pour une rotation continue
Un servomoteur normal tourne à environ 180 degrés. De toute évidence, nous ne pouvons pas l'utiliser pour un véhicule roulant sur roues.Etapes pour retirer le limiteur du servo et le faire tourner à 360 degrés, afin que vous puissiez l'utiliser comme si vous utilisiez un moteur à courant continu!
Le limiteur actuel est constitué de 2 parties: le potentiomètre et la boîte de vitesses. Ce que nous devons faire, c'est casser la connexion du potentiomètre avec la carte de circuit imprimé interne et retirer un bouton d'un pignon de la boîte de vitesses.
 |  |
| Retirer du couvercle et de la boîte de vitesses | Dessouder, puis Retirer le moteur à courant continu et le potentiomètre |
 |  |
| Remplacement du potentiomètre par deux résistances, soit la moitié de la valeur du potentiomètre Ici 2,7kΩ | Couper la patte qui dépasse de l'engrenage |
Récupérer la position d'un SG90
A l'intérieur du SG90
Un servomoteur est constitué d'un moteur avec réducteurs d'une carte électronique et d'un potentiomètre linéaire qui permet à la carte électronique de vérifier la position actuelle du servo.Je vous propose d'utiliser cette valeur envoyée par le potentiomètre afin de connaitre la position du servomoteur.
En effet le potentiomètre est mécaniquement lié directement au palonnier du servomoteur.
Donc la résistance obtenue au bornes du potentiomètre correspond à la position du palonnier.
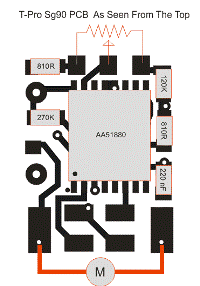 | 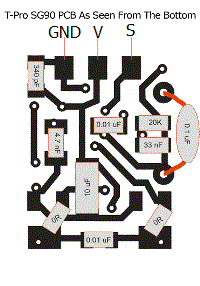 |  |
Il suffit pour cela de souder un fil sur la patte du milieu du potentiomètre. Ensuite une fois le servomoteur en action, on peut mesurer la tension entre la masse en notre nouvelle broce du servo (patte du milieu du potentiomètre) d'environ 0.9V lorsque le palonnier est tourné tout a droite, et 1,7V lorsque le palonnier est tout a gauche.
Le programme devra évidement effectuer un genre d'étalonnage au début de l'exécution.
Positionner le servo tout a droite, et voire la valeur du capteur, puis positionner le servo à gauche et voir la valeur du capteur.
Ces deux valeurs vont nous servir de référence min et max de la variation.
En effet la variation mesurée est de 1.7V - 0.9V = 0.8V. Votre entrée analogie doit avoir une définition suffisante pour avoir un peu de précision.
En effet sur une variation de 0.8V il s'agit de représenter théoriquement les 180° de rotation. Donc l'entrée analogique devra être capable de repérer des variations de 5mV pour avoir une précision d'environ 1°.
Il va de sois qu'il est aussi envisageable d'enregistrer les valeurs minimales et maximales de la tension obtenue au bornes du potentiomètre pour ne pas avoir a effectuer l'étalonnage a chaque initialisation.
Les moteurs Nema
Les désignations
Un moteur NEMA (National Electrical Manufacturers Association)Nous prendrons comme exemple : 17HS2408 NEMA DDMMLLL–CCCIVVVSSSW
| DD | Dimensions du moteur, son diamètre ou longueur côté du carré de la face avant, hors tout, exprimé en dixièmes de pouce ,arrondi. Exemple pour un NEMA17 : $1,7\times25,4=43,18mm$ |
| MM | type de montage (pouce x 10)+diamètre, "C" trous taraudés en façade "D" tôle arriere |
| LLL | LLL : longueur (pouce x 10) |
| - | séparation |
| CCC | courant par phase (A x 10) |
| I | classe d'isolation, définit la temp max de travail en °F
|
| VVV | Tension par phase (V x 10) |
| SSS | Nombre de pas/tour |
| W | code bobinage
|
Nema 8, 11, 14, 17, 23, 24, 34 et 42
La fréquence d'utilisation d'un NEMA17 est d'environ 8000Hz - 150.00 tr/min
Branchement 17HS2408
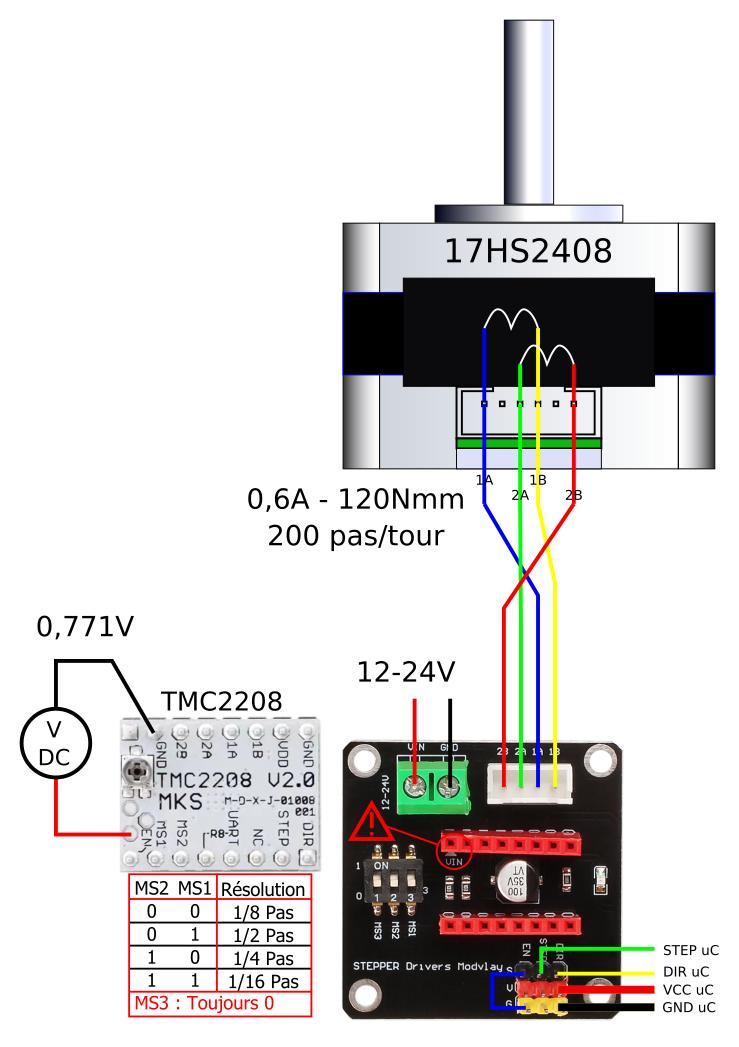
Bien que le moteur pas à pas que nous utiliserons ici 17HS2408 est soit conçu pour 0,6A, nous ne devons jamais le régler à sa capacité de courant maximale.
Il est fortement recommandé de réduire la quantité de courant vers le moteur d'au moins 10 %, ce qui dans notre cas se traduirait par environ 0,54 A.
TMC2208
$Vref=I\cdot \sqrt{2}=\dfrac{0,6}{1.1}\times \sqrt{2}=0,771V$
A4988
$Vref=I\times 0,8=\dfrac{0,6}{1.1}\times 0,8=0,436V$
DRV8825
$Vref=\dfrac{I}{2}=\dfrac{0,6}{2.2}=0,273V$
| Angle par pas deg | Courant A | Résistance/phase Ω | couple de maintien Nmm | Nombre de fils |
|---|---|---|---|---|
| 1.8 | 0.6 | 8 | 120 | 4 |
La fixation se fait par 4 taraudage M3 positionner tous les 31mm
Drivers
| A4988 | DRV8825 | LV8729 | TMC2208 | TMC2100 | TMC2130 | |
|---|---|---|---|---|---|---|
| Courant par default | 2A | 1.3A | 0.8A | 0.7A | 0.5A | 0.76 |
| Vref par default | 0.8V | 0.65V | 0.4V | 1V | 0.65V | 1V |
| Courant Maxi | 2A | 2.5A | 1.5A | 1.41A | 1.2A | 2A |
| Formule | $i=\dfrac{V_REF}{0.8}$ | $i=V_REF\times 2$ | $i=\dfrac{V_REF}{\sqrt 2}$ | $i=\dfrac{V_REF\times 1.9}{2.5}$ | ||
| Ajustement du courant | Horaire Augmente Anti-horaire Diminue | Horaire Diminue Anti-horaire Augmente | Horaire Augmente Anti-horaire Diminue | |||
| Micropas | 1, 1/2, 1/4, 1/8, 1/16 | 1, 1/2, 1/4, 1/8, 1/16, 1/32 | 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128 | 1, 1/2, 1/4, 1/8, 1/16 | 1/16 | 1, 1/2, 1/4, 1/8, 1/16, 1/256 |
| Moteur | 8V-35V | 8.2V-45V | 6V-36V | 4V-35V | <1.2A | 4.75V-46V |
| Spécifications | Pas cher | Courant fort | Silencieux | Silencieux, lissage | ||
Pour cela il faut calibrer la tension $V{REF}$, celle-ci se prends entre le GND et le potentiomètre (Et oui, directement dessus). En débranchant le moteur, il y a juste à alimenter le composant.
Concernant les drivers, le DRV8825 offre une résolution micro-stepping au 1/32 de pas; le A4988 est limité à 1/16 de pas.
Les broches de sélection activée pour le mode 1/16 de pas sur le A4988 correspond à 1/32 de pas sur le DRV8825. A l'exception de ce cas, toutes les autres configurations M0-M1-M2 de résolutions micro-stepping sont identiques sur le DRV8825 et le A4988.
Les impulsions STEP HAUT et BAS doivent avoir un temps d'au moins 1.9 µs; mais peut descendre jusqu'à 1 µs avec un A4988
Le DRV8825 supporte une tension maximale plus élevée qu'un A4988 (45 V contre 35 V).
Driver A4988
$V_{REF}=8\cdot I_{MAX} \cdot R_{CS}$
$R_{CS}$ est la résistance de détection de courant; Les versions originales de cette carte utilisaient des résistances de détection de courant de 0,050 Ω, mais le fabricant est passés à des résistances de détection de courant de 0,068 Ω en janvier 2017, ce qui rend plus utile la plage du potentiomètre de réglage.
Ainsi, par exemple, si vous souhaitez régler la limite de courant à 1 A et que vous avez une carte avec des résistances de détection de 68 mΩ, vous définirez VREF sur 540 mV. Cela garantit que même si le courant à travers chaque bobine change d'un pas à l'autre, l'amplitude du vecteur de courant dans le moteur pas à pas reste constante à 1 A:
$\sqrt{I_{COIL1}^2 + I_{COIL2}^2}= I_{MAX}= 1 A$
Si vous souhaitez au contraire que le courant traversant chaque bobine soit de 1 A en mode pas à pas complet, vous devez définir la limite de courant à 40% plus élevée, ou 1,4 A, car les bobines sont limitées à environ 70% du courant défini limite en mode pas à pas (l'équation ci-dessus montre pourquoi c'est le cas). Pour ce faire avec une carte avec des résistances de détection de 68 mΩ, vous devez régler VREF à 770 mV.
$V_{REF}=8\times 0,6 \times0,068=0,3264V$
Driver DRV8825
Pour mon 17HS2408, $V_{REF}=\dfrac{0,6}{2}=0,3V$
Avec 10% de marge cela fait 0,27V
Détails
| Moteur | A4988 (Imax=2A) | A8825 (Imax=2,5A) | |||||
|---|---|---|---|---|---|---|---|
| Imoteur | Inom (71%) | R050 | R100 | R200 | R050 | R100 | R200 |
| Vref (mV) | Vref (mV) | ||||||
| 0,1 | 0,07 | 28 | 56 | 112 | 17 | 35 | 70 |
| 0,2 | 0,14 | 56 | 112 | 224 | 35 | 70 | 140 |
| 0,3 | 0,21 | 84 | 168 | 336 | 52 | 105 | 210 |
| 0,4 | 0,28 | 112 | 224 | 448 | 70 | 140 | 280 |
| 0,5 | 0,36 | 144 | 288 | 576 | 90 | 180 | 360 |
| 0,6 | 0,43 | 172 | 344 | 688 | 107 | 215 | 430 |
| 0,7 | 0,50 | 200 | 400 | 800 | 125 | 250 | 500 |
| 0,8 | 0,57 | 228 | 456 | 912 | 142 | 285 | 570 |
| 0,9 | 0,64 | 256 | 512 | 1 024 | 160 | 320 | 640 |
| 1,0 | 0,71 | 284 | 568 | 1 136 | 177 | 355 | 710 |
| 1,1 | 0,78 | 312 | 624 | 1 248 | 195 | 390 | 780 |
| 1,2 | 0,85 | 340 | 680 | 1 360 | 212 | 425 | 850 |
| 1,3 | 0,92 | 368 | 736 | 1 472 | 230 | 460 | 920 |
| 1,4 | 0,99 | 396 | 792 | 1 584 | 247 | 495 | 990 |
| 1,5 | 1,07 | 428 | 856 | 1 712 | 267 | 535 | 1070 |
| 1,6 | 1,14 | 456 | 912 | 1 824 | 285 | 570 | 1 140 |
| 1,7 | 1,21 | 484 | 968 | 1 936 | 302 | 605 | 1 210 |
| 1,8 | 1,28 | 512 | 1 024 | 2 048 | 320 | 640 | 1 280 |
| 1,9 | 1,35 | 540 | 1 080 | 2 160 | 337 | 675 | 1 350 |
| 2,0 | 1,42 | 568 | 1 136 | 2 272 | 355 | 710 | 1 420 |
| 2,1 | 1,49 | 372 | 745 | 1 490 | |||
| 2,2 | 1,56 | 390 | 780 | 1 560 | |||
| 2,3 | 1,63 | 407 | 815 | 1 630 | |||
| 2,4 | 1,70 | 425 | 850 | 1 700 | |||
| 2,5 | 1,78 | 445 | 890 | 1 780 | |||
Driver TMC2208

Leur courant ce règle en RMS et non pas en continu, donc pour, par exemple, un moteur qui consomme 1.5A par phase nominal, il faut convertir ce courant en RMS, ce qui ce fait en divisant par $\sqrt 2$
Exemple pour 1,5A, $RMS=\dfrac{1,5}{\sqrt 2} = 1,06A$, c'est la valeur que l'on utilise pour régler le Vref des TMC2xxx, donc on règle Vref à 1.06V.
Ne pas oublier que les Imax pour les 2100 et 2130 sont de 1.2A RMS max, donc Vref à 1.2V max (Inom de 1.7A max) et pour le 2208 de 1.4A RMS max, donc Vref à 1.4V max (Inom de 2A max).
| MS2 | MS1 | Pas | Interpolation | Mode |
| 0 | 0 | 1/8 | oui jusqu'à 256 | Stealthchop2 |
| 0 | 1 | 1/2 | oui jusqu'à 256 | Stealthchop2 |
| 1 | 0 | 1/4 | oui jusqu'à 256 | Stealthchop2 |
| 1 | 1 | 1/16 | oui jusqu'à 256 | Stealthchop2 |
Le mode UART
Les avantages du mode UART:- Le courant du moteur peut être réglé arbitrairement par le micrologiciel.
- Les micro-étapes peuvent être définies arbitrairement par le micrologiciel (jusqu'à 256 micro-étapes réelles)
- Les micropas réels et interpolés peuvent être combinés pour obtenir
- Le micrologiciel peut basculer dynamiquement les moteurs pas à pas entre les modes stealthChop2 et spreadCycle via UART.>/li>
- Lorsque le moteur ne bouge pas, le courant de veille du moteur peut être réduit dynamiquement (via UART).
"spreadCycle™"-for high speed and high dynamics
Mode de transmission
chaque octet est LSB ... MSB, premier octet transmis| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 |
| Sync + Reservé | Adresse Esclave | R/W Registre 7bits | 32 bits données | CRC | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 0 | 1 | 0 | Réservé (sans souci mais inclus dans le CRC) | SLAVEADDR=0 | Adresse du registre 7bits | 1 | octets de données 3, 2, 1, 0 (octet haut à bas | CRC | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chaque transmission permet une synchronisation du diviseur de débit en bauds interne avec l'horloge maître.
La vitesse de transmission réelle est adaptée et les variations de la fréquence d'horloge interne sont compensées.
Ainsi, le débit en bauds peut être librement choisi dans la plage valide.
Chaque octet transmis commence par un bit de démarrage (logique 0, niveau bas sur SWIOP) et se termine par un bit d'arrêt (logique 1, niveau haut sur SWIOP).
Le temps de bit est calculé en mesurant le temps entre le début du bit de début (transition 1 à 0) et la fin de la trame de synchronisation (transition 1 à 0 du bit 2 au bit 3). Toutes les données sont transmises par octet. Les mots de données de 32 bits sont transmis avec l'octet le plus élevé en premier.
Une vitesse de transmission minimale de 9000 bauds est autorisée, en supposant une horloge de 20 MHz (pire des cas pour une faible vitesse de transmission).
Le débit en bauds maximum est de fCLK / 16 en raison de la stabilité requise de l'horloge en bauds.
L'adresse esclave SLAVEADDR est toujours 0 pour le TMC22xx.
Documentation complète
Vitesse et accélération
source : embeddedUn nouvel algorithme d'accélération des moteurs pas à pas permet de paramétrer et de calculer des profils de vitesse en temps réel.
Cet algorithme peut fonctionner sur un microcontrôleur bas de gamme en utilisant uniquement des opérations arithmétiques à virgule fixe simples et aucune table de données.
Il développe une approximation précise de la synchronisation d'une rampe linéaire avec une accélération et une décélération constantes.
La fréquence de la minuterie du microcontroleur doit être la plus élevée que possible tout en permettant de longs délais lorsque le moteur est accéléré à partir de l'arrêt.
Une fréquence de minuterie de 1MHz a été utilisée. Une vitesse maximale du moteur de 300 tr/min équivaut alors à un compte de retard de 1 000.
Il est nécessaire d'avoir une résolution de minuterie élevée pour donner une accélération douce à grande vitesse.
Notation et formules de base
Retard (sec) programmé par le compteur de temps $c$ :| Equation 1 | $\delta t=\dfrac{c}{f}$ | $f$ = fréquence de la minuterie (Hz). |
| Equation 2 | $\omega=\dfrac{\alpha\cdot f}{c}$ | $\omega$ angle de pas du moteur (radian) $1~rad = 180 /\pi = 57,3 \deg$ $1~rad\cdot s^{-1} = 30 /\pi = 9,55~tr\cdot min^{-1}$. |
| Equation 3 | $\omega \prime =\dfrac{2\dot \alpha\cdot f^2\cdot (c_1-c_2)}{c_1\cdot c_2 \cdot (c_1+c_2)}$ | $\omega$ angle de pas du moteur (radian) $1~rad = 180 /\pi = 57,3 \deg$ $1~rad\cdot s^{-1} = 30 /\pi = 9,55~tr\cdot min^{-1}$. |
Rampe de vitesse linéaire—exacte
Sur une rampe linéaire, l'accélération' est constante et la $vitesse(t) = \omega \prime \cdot t$. L'intégration donne l'angle d'arbre moteur ( t ):| Equation 4 | $\theta(t)=\int_{0}^{t}\omega(\tau)d\tau=\dfrac{\omega'\cdot t^2}{2}=n\cdot\alpha$ | $n≥ 0$ numéro de pas (réel). Lorsque l'arbre est à $\theta = n\cdot\alpha$, (entier n ) est la n ième impulsion de pas. |
| Equation 5 | $t_n=\sqrt{\dfrac{2\cdot n\cdot \alpha}{\omega'}}$ | Le décompte exact de la minuterie pour programmer le délai entre les n ième et (n + 1) ième impulsions ($n≥0). |
| Equation 6 | $C_n=f\cdot (t_{n+1}-t_n)$ | Le compte initial $c_0$ se factorise pour donner les équations 7 et 8 :. |
| Equation 7 | $C_0=f\sqrt{\dfrac{2\alpha}{\omega'}}$ | |
| Equation 8 | $C_n=C_0(\sqrt{n+1}-\sqrt{n})$ |
En temps réel, l'équation 8 nécessiterait le calcul d'une racine carrée pour chaque étape, avec le problème supplémentaire de perte de précision par soustraction.
GRBL
- G0, G1: Mouvements linéaires
- G2, G3: Mouvements d’arc et hélicoïdaux
- G4: Temporisation
- G10 L2, G10 L20: Définir les décalages des coordonnées de travail
- G17, G18, G19: Choix du plan de travail
- G20, G21: Unités
- G28, G30: Aller à la position prédéfinie
- G28.1, G30.1: Définir une position prédéfinie
- G38.2: Mesure au palpeur
- G38.3, G38.4, G38.5: Mesure au palpeur
- G40: Révocation de la compensation de rayon d’outil
- G43.1, G49: Compensation dynamique de longueur d’outil
- G53: Déplacements en coordonnées machine (Absolues)
- G54, G55, G56, G57, G58, G59: Choix du système de coordonnées
- G61: Mode trajectoire exacte
- G80: Révocation des codes modaux
- G90, G91: Types de déplacement
- G91.1: Mode de déplacement relatif pour les offsets I, J et K
- G92: Décalages d’origines avec mise à jour des paramètres
- G92.1: Révocation des décalages d’origine
- G93, G94: Modes d’avance
- M0, M2, M30: Pause et fin du programme
- M3, M4, M5: Contrôle de la broche
- M7* , M8, M9: Contrôle du liquide de refroidissement
- M56* : Commande de neutralisation du mouvement de stationnement
Changer le G54 (10,10,Z0.5)
G10L2P1X10Y10Z0.5 G54 (10,10,Z0.5)
G10L2P2X10Y10Z0.5 G55 (10,10,Z0.5)
G10L2P3X10Y10Z0.5 G56 (10,10,Z0.5)
G10L2P4X10Y10Z0.5 G57 (10,10,Z0.5)
G10L2P5X10Y10Z0.5 G58 (10,10,Z0.5)
G10L2P6X10Y10Z0.5 G59 (10,10,Z0.5)
Décallage d'origine G92
G92X0Y0Z0 à la position ou je me trouve
Longueur d'outil a 50
G43.1 Z50 pour selectionner l'outil T1
G2(sens horaire), G3 (sens anti-horaire) Interpolation circulaire en vitesse travail G2 ou G3 axes décalages (format centre) G2 ou G3 axes R- (format rayon) G2 ou G3 décalages
G0 G90 X100 Y0
G1 Y100 F200
G2 X150 Y150 I50 J0
G2 X200 Y100 I0 J-50
G1 Y0
X100
Moteur 24BYJ-48
20BYJ-48/ 24BYJ-48 /28BYJ-48
C'est une question de diamètre Ø20mm pour le 20BYJ-48, Ø24mm pour le 24BYJ-48, et Ø28 pour le 28BYJ48.Caractéristique des moteurs pas à pas 24BYJ-48
- Alimentation : 5 Vcc
- Résistance: 16,5 Ω
- Intensité: 300 mA
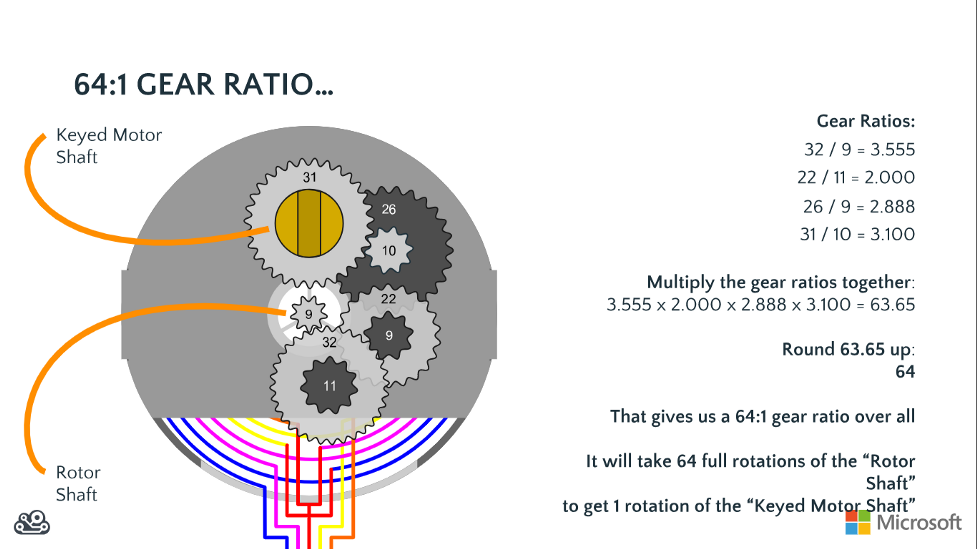
- Réduction: 1/32
- Nombre de pas: 64 (réduction de 2048 en sortie d'axe)
- Frequence : 100Hz → 2.93 tr/min
- Couple: 39 mNm
- Niveau sonore: 40 dB.
- Entraxe de fixation: 31 mm
- Axe: Ø 5 mm avec double méplat (épaisseur 3 mm)
- Longueur de l'axe: 8 mm
- Masse : 35gr
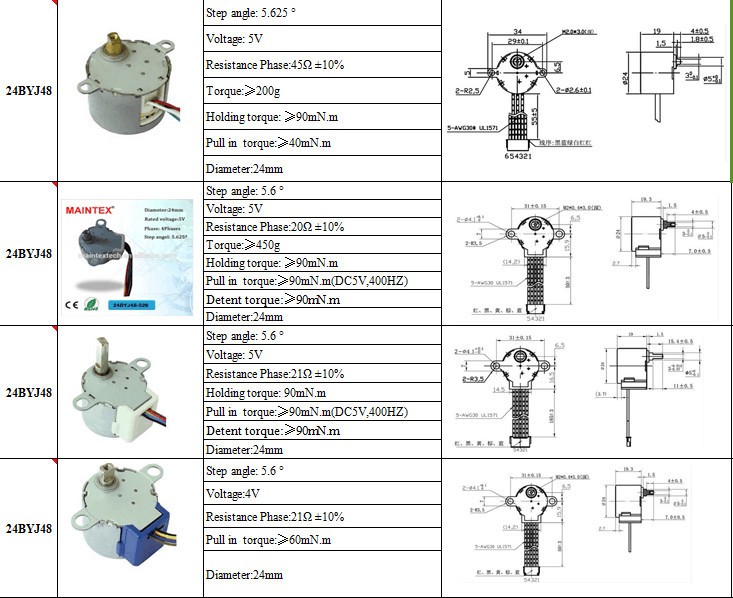
Câblage du 24BYJ-48
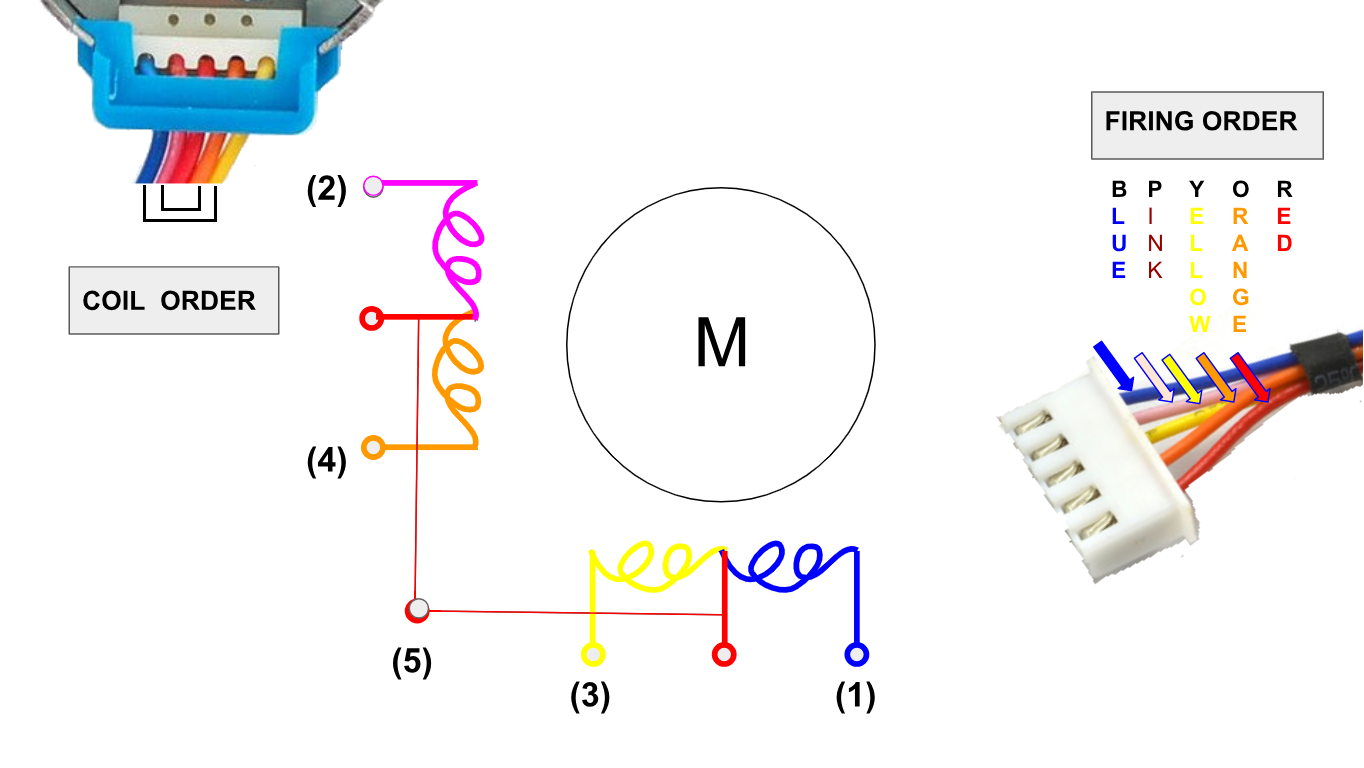
Engrenages internes 24BYJ-48
24BYJ-48 un autre pilote
 Il est important que le courant maximale soit prévu dans le driver, sinon le moteur chauffe, vibre voir décède, snif...
Pour cela il faut calibrer la tension $V_{ref}$, celle-ci se prends entre le GND et le potentiomètre (Et oui, directement dessus).
Il est important que le courant maximale soit prévu dans le driver, sinon le moteur chauffe, vibre voir décède, snif...
Pour cela il faut calibrer la tension $V_{ref}$, celle-ci se prends entre le GND et le potentiomètre (Et oui, directement dessus).En débranchant le moteur, il y a juste à alimenter le composant.
$I_{moteur}=300mA$ auquel on enlève 10% pour éviter les échauffements moteur soit $0.27A$
DRV8825
$i=V_{ref}\times 2$
$V_{ref}=\dfrac{I_{moteur}}{2}=0,135V$
A4988
$i=\dfrac{V_{ref}}{0.8}$
$V_{ref}=I_{moteur}\times 0.8 =0,338V$
TMC2208
$i=\dfrac{V_{ref}}{\sqrt{2}}$
$V_{ref}=I_{moteur}\times \sqrt{2} =0,382V$
Le moteur Brushless
Comme son nom l'indique un moteur Brushless ne comporte pas de balais, c'est une machine synchrone à aimants permanents.Suivant les technologies, les aimants peuvent se trouver sur le Stator ou le Rotor.Le rapport poids/puissance est très favorable par rapport aux moteurs à courant continu.
Caractéristiques des moteurs Brushless
Il faut tout d'abord savoir que le rendement d'un moteur Brushless est de 75 à 95%.Ce sont souvent des moteurs à 3 phases, U, V et W, la séquences comporte 6 étapes de 60°
Le rotor, alimenté en courant continu, par un système de contacts glissants (bagues), crée un champ magnétique rotorique qui suit le champ tournant statorique avec un retard angulaire θ lié à la charge (plus la charge est importante, plus θ est grand).
Étant donné que le rotor tourne à la même vitesse que le champ tournant, ce moteur ne peut pas être démarré directement sur le réseau 50 Hz.
On peut utiliser un convertisseur de fréquence dont la fréquence augmente progressivement lors de la phase de démarrage (rampe).
Le pilotage
PWM (Modulation de largeur d'impulsion)
Carte de programmation
- CutOffVoltage :Permet de plafonner le seuil mini d'alimentation avant coupure, afin de ne pas dégradé la batterie Lipo. 3.4V par cellule pour protection
- Puch Mode : de 1 à 9, permet de déterminer la rampe d'accélération, 9 instantané, 1 montée lente de l'accélération
- Timing : Avance à l'allumage,
- BreakForce : de 0 à 40%
- Reverse Force : Force de la marche arrière 0 à 100%
- Neutrale range : Tolérance de pilotage, 5% environs pour les voitures, en pilotage manuel
- Inverse : Paramètre d'inversion
Couple moteur et ESC
ESC (Electronic Speed Controller)
Les batteries
Batterie NiMh
Elle est composé de plusieurs éléments de 1.2V.
de 1 à 4Ah.
Batterie LiPo
Les batteries Lithium Polymère. Elle est composé de plusieurs cellules de 3,7V.
Le nombre de S est le nombre de cellules, 1S 3,7V, 2S 7,4V, 3S 11,1V,4S 14,8V
La capacité donée en Ah, soit le nombre d'ampère durant une heure Exemple utilisé une batterie : 5Ah.
La capacité de décharge instantannée C, exemple 40 à 50C soit 40x5=200A et 50x5=250A (très peu de temps 10 à 15s).
La capacité de charge, entre 1 et 5C, si elle à 5C on peut la charger en 5x5=25A.
Il y a quelquefois des fils supplémentataires de façon à équilibrer la charge.
Lors de la charge utiliser un sac à lithium.
Si il y a surcharge d'une batterie lipo, il y a risque d'exploision.
Batterie lithium fer phosphate
LFP couramment appelé simplement accumulateur LiFe.
Elles supportent des intensités élevées ce qui leur permet à la fois de fournir beaucoup de puissance et d'être rechargées rapidement.
Les batteries au lithium fer phosphate () sont les plus sûres parmi les batteries au lithium-ion traditionnelles. La tension nominale d'une cellule LFP est de 3,2 V (au plomb : 2 V/cellule). Une batterie LFP de 12,8 V est composée de 4 cellules connectées en série.
Calcul du couple des moteurs
Couple en kg.cm Nombre de KV en kV à vide Vitesse en tr.min-1 Tension en V Diamètre de roue en mm
Fabriquer un moteur Brushless
Commençons par le moteur parfait, sans pertes, η=1
structure simplifiée du rotor d’un moteur électrique

Un rotor est constitué d’un cylindre en fer doux (perméable au champ magnétique) de longueur l dans lequel on a fait des encoches, ici trois (mais il peut y en avoir un nombre quelconque, trois et douze étant très courants en modélisme). On place des bobines en fil de cuivre autour des parties saillantes appelées pôles.
On ne considère que la longueur des conducteurs éctiligne, le long des pôles. 
Ici, un rotor à P = 4 pôles et des bobines à n = 3 spires, ce qui est équivalent à utiliser 4x3x2 = 24 conducteurs rectilignes de longueur L.
En mécanique le couple s'exprime : $C=F\cdot R$
En électricité :(1) $C=I\cdot k\cdot B \cdot 2 \cdot P\cdot n \cdot L \cdot R$
La vitesse mécanqiue : $\omega=\dfrac{\pi \times N}{30}=\dfrac{V}{R}$
En électricité :(2) $\omega=\dfrac{E}{k\cdot B \cdot 2 \cdot P\cdot n \cdot L \cdot R}$
$R$ étant le rayon du rotor en m,$L$ la longueur du conducteur en m, $F$ la force en Newton, $C$ en Nm,
$E$ la tension en Volt, $I$ courant constant en ampère
$B$ l'induction magnétique en Tesla
$P$ le nombre de pôles et à $n$ le nombre de spires par pôles.
Le coefficient $k$ permet de tenir compte du fait que périodiquement et à tour de rôle chaque bobine est déconnectée et n’agit donc plus, mais également prendre en compte les diverses façons de câbler les bobines entre elles.
(1) $F=I \cdot B\cdot L$ avec (2) $E=F \cdot B\cdot L$ avec
Le pas polaire
On définit le pas polaire du moteur, comme étant le nombre d’encoches sous un pôle.
$P$ le nombre de pôles Nombre d'encoches
Sections des fil émaillé
Diamètre Masse
liéïque Section
mm² 2 fils
parallèles
3 fils
parallèles Centième mm gr/m 10 0,10 0,070 0,008 0,016 0,024 12 0,12 0,101 0,011 0,023 0,034 14 0,14 0,137 0,015 0,031 0,046 16 0,16 0,179 0,020 0,040 0,060 18 0,18 0,226 0,025 0,051 0,076 20 0,20 0,279 0,031 0,063 0,094 22.4 0,22 0,350 0,039 0,079 0,118 25 0,25 0,436 0,049 0,098 0,147 28 0,28 0,547 0,062 0,123 0,185 30 0,30 0,628 0,071 0,141 0,212 35.5 0,36 0,880 0,099 0,198 0,297 40 0,40 1,117 0,126 0,251 0,377 45 0,45 1,414 0,159 0,318 0,477 50 0,50 1,746 0,196 0,393 0,589 56 0,56 2,190 0,246 0,493 0,739 63 0,63 2,771 0,312 0,623 0,935 65 0,65 2,950 0,332 0,664 0,995 67 0,67 3,134 0,353 0,705 1,058 71 0,71 3,520 0,396 0,792 1,188 75 0,75 3,927 0,442 0,884 1,325 80 0,80 4,469 0,503 1,005 1,508 85 0,85 5,045 0,567 1,135 1,702 90 0,90 5,656 0,636 1,272 1,909 95 0,95 6,301 0,709 1,418 2,126 100 1,00 6,982 0,785 1,571 2,356 106 1,06 7,845 0,882 1,765 2,647 112 1,12 8,758 0,985 1,970 2,956 118 1,18 9,722 1,094 2,187 3,281 120 1,20 10,054 1,131 2,262 3,393 125 1,25 10,910 1,227 2,454 3,682 130 1,30 11,800 1,327 2,655 3,982 140 1,40 13,685 1,539 3,079 4,618 150 1,50 15,710 1,767 3,534 5,301 160 1,60 17,874 2,011 4,021 6,032 170 1,70 20,179 2,270 4,540 6,809 180 1,80 22,622 2,545 5,089 7,634
Si le nombre de pôle est petit, on obtient un régime fort et un faible couple, si il est grand on obtient un grand couple et un faible régime.
Le nombre de pôles P agit donc ni plus ni moins que comme un réducteur électromagnétique.
Les valeurs classiques de P sont données dans le tableau 4 avec en vis-à-vis les régimes de rotation correspondants maximaux en général admis pour les moteurs « brushless ».
Représentation d'une Bobine dans le stator
Diamètre du fils
Résistivité du matériaux
Matériau Résistivité ρ
x 10-8 Ωm Matériau Résistivité ρ
x 10-8 Ωm argent 1,6 platine 10 cuivre 1,7 fer 10 or 2,4 silicium 10 aluminium 2,7 étain 18 magnésium 4,6 plomb 21 tungstène 5,6 germanium 46 zinc 6 constantan 49 nickel 7 mercure 96 laiton 7 nichrome 100 cadmium 7,6 carbone 3500
Calcul de la résistance électrique d'un fil
Choisir la matière : 1.7 x 10-8 Ωm²/m Choisir le diamètre en Centième: 0.1 mm soit 0.008 mm2 Longueur : m Résistivité 43.290 Ω, Masse 1.396 gr
Couplage des moteurs en étoile et triangle.
Un moteur avec enroulements en triangle (Δ) donne un faible couple à basse vitesse, mais permet des vitesse de pointe plus élevée.
La configuration étoile (λ) donne un couple élevé à bas régime, mais des vitesse de pointe plus faible.
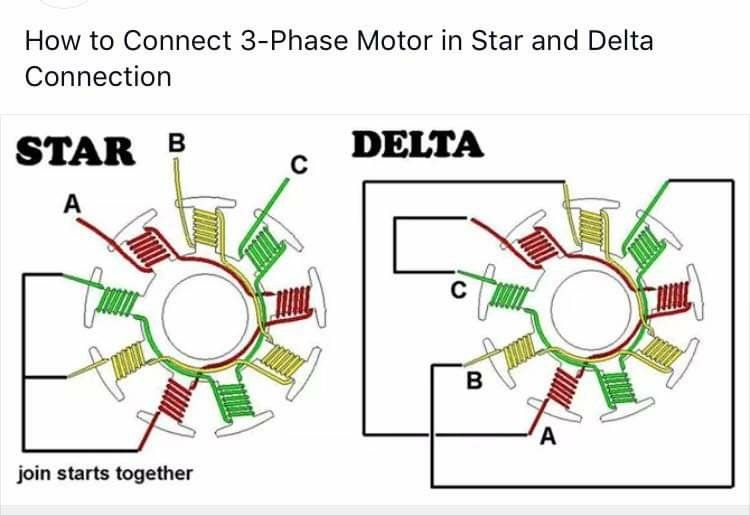
Connexion Tension phase U_phase Courant phase I_phase Couple max Star (Y) U_line / √3 I_line 0.577 × Δ Delta (Δ) U_line I_line / √3 1.732 × Y
En gros, triangle donne ~1.73× plus de couple pour même tension, mais chauffe beaucoup plus.
Nombre de bobines, nombre de pôles, nombre d'encoches
Avec une bobine on peut donc faire 2 pôles et pour faire plusieurs pôles (chiffre pairs) il faut donc plusieurs bobines. Dans un bobinage de stator il devra y avoir logiquement autant de bobines que de paires de pôles. Ainsi pour 2 pôles il y aura 1 bobine, pour 4 pôles il y aura 2 bobines, pour 6 pôles 3 bobines, ect…
Chaque bobine occupe 2 encoches et il faut donc le double d'encoches que du nombre de bobines. Ce nombre est aussi à multiplier par le nombre de phases pour lequel le moteur va pouvoir être branché : monophasé (1phase), biphasé (2 phases), triphasé (3phases).
Les stators sont donc conçus avec un nombre d'encoches compatible avec le nombre de phase et de pôles.
Le nombre standard d'encoches dans les stators est : 6, 12, 18, 24, 36, 48, 72, pour les plus courantes
Nombre spéciaux : 30, 32, 42, 60
En triphasé, Possibilités d'exécution en encoches entières dans le bobinage Nombre d'encoches Nombre d'encoches par phase Nombre de pôle P 6 1 2 12 1 4 12 2 2 18 1 6 18 2 3 18 3 2 24 1 8 24 2 4 24 4 2 36 1 12 36 2 6 36 3 4 36 4 3 36 6 2 48 1 16 48 2 8 48 4 4 48 8 2 72 1 24 72 2 12 72 3 8 72 4 6 72 6 4 72 8 3 72 12 2

Suivant le nombre d'encoches attribué par pôle, la bobine peut se constituer de plusieurs sections, chaque section occupant plusieurs encoches.
Dans un stator les bobines sont logées dans des encoches. Sur un schéma de bobinage on représente le stator déroulé à plat.
Dans sa partie supérieure, un schéma de bobinage renseigne sur:
- le nombre d'encoches
- le nombre de bobines
- le pas des bobines
Dans sa partie inférieure, le schéma de bobinage renseigne sur :
- les connexions (liaisons entre bobines)
- les interconnexions (liaisons entre sections de bobines)
Flux magnétique
Faisons un calcul « à la louche » :
La tension induite est donnée par la loi de Faraday :
V = N. ΔΦ/Δt.
Φ est le flux magnétique : le produit du champ magnétique par la surface.
ΔΦ est la variation du flux dans le temps Δt.
N est le nombre de spires qui entourent le flux.
Prenons un aimant au néodyme dont le champ est 1 tesla et de surface 1 cm².
Le flux qui traverse sa surface est 10^-4 weber.
Si vous faites passer une bobine de 10 tours et de 1 cm² de section devant l’aimant, en 0,1 secondes, la tension induite sera :
10*10^-4/0,1 = 0,01 volts.
Données physiques des aimants
N52 : Br=14200-14700 Gauss ou 1.42-1.47 Tesla
La densité du flux magnétique s'appelle également induction magnétique ou champ B. L'unité de l'induction magnétique est le tesla (unité SI) ou le gauss (10 000 Gauss = 1 Tesla).
Formule pour la densité de flux parallélépipède magnétique
$B=\dfrac{B_r}{\pi}\biggl[ arctan\biggl(\dfrac{L\cdot W}{2\cdot z \sqrt{4z^2+L^2+W^2}}\biggr)-arctan\biggl(\dfrac{L\cdot W}{2(D+z)\sqrt{4(D+z)^2+L^2+W^2}} \biggr)\biggr]$
$B_r$ : Champ rémanent, indépendant de la géométrie de l'aimant (voir Données physiques de l'aimant)
$z$ : Distance de la surface du pôle sur l'axe de symétrie
$L$ : Longueur du parallélépipède
$W$ : Largeur du parallélépipède
$D$ : Epaisseur (ou hauteur) du parallélépipède
L'unité de longueur peut être choisie librement, mais à condition qu'elle soit la même pour toutes les longueurs.
Exemple pour un aimant de N52 40x10x4 nous prendrons
$\Phi=$0,291Wb à 0,301Wb, à 1mm de distance $\Phi$=0,249Wb à 0,258Wb
Formules diverses
$U = -N\cdot \dfrac{\Delta(B\cdot A)}{\Delta t}$
$N$ nombre de spires
$B$ champe magnétique des aimants
$A$ section d'une bobine de cuivre $A=\pi (R^2-r^2)$
$E=\dfrac{1}{2}\cdot L \cdot i^2$
- E : l'énergie en Joule (J)
- L : l'inductance de la bobine en Henry toujours (H)
- i : l'intensité du courant parcourant la bobine, en Ampères (A)
une bobine de longueur l, qui possède N spires de surface de section S :
$L=\mu \cdot \dfrac{N^2}{l}\cdot S$
- L : inductance de la bobine en Henry (H)
- N : nombre de spires de la bobine
- l : longueur de la bobine (et non pas du fil qui la compose) en mètres (m)
- S : section de la bobine (de son fil, ici) en mètres carrés (m²)
- μ : perméabilité magnétique du milieu autour duquel sont enroulées les spires
Pour le vide (ou pour l'air "sec"), ce paramètre s'appelle $μ_0$ et est égal à $4\cdot 10^{−7}~H\cdot m^{−1}$.
Unité Henry/m ou newton par ampère carré ($N\cdot A^{−2}$).
Cobalt $\mu_r=250~H\cdot m^{−1}$
Fer $\mu_r=5 000~H\cdot m^{−1}$
Mu-métal $\mu_r=100 000~H\cdot m^{−1}$
Nickel $\mu_r=600~H\cdot m^{−1}$
Paramètres moteur Brushless:
Kv= RPM/Volt.
- Rm= resistance moteur en Ohms.
- Io= Courant sans charge.
Kq= 30/(pi Kv)
Kq= Couple constant en Nm
N= Kv(I – Io) en RPM
Q= Kq(I – Io) en Nm
η= (V- I Rm)(I - Io)/(V I)
V et I tension et courant en travail.
Imax= sqrt(V Io/Rm)
Qmax= Kq (Imax – Io)
RPMmax= Kv( V – Imax Rm)
ESC
Paramètres utiles existants :
- Low Voltage Limiter : permet de définir une tension de coupure des moteurs.
Si vous mettez 3.2V/cell l’ESC va couper l’alimentation si la tension des cellules de la lipo descend sous les 3.2V (9.6V au total). Peut causer une chute du drône si vous ne surveillez pas cette tension.
Il est conseillé de mettre la valeur à Off.
- Temperature Protection : Laisser à “Off” car il me semble que nos ESC ZTW ne possèdent pas de capteurs thermiques.
- PWM Frequency/Damped : Sélectionner la valeur Damped Light.
Cette fonction permet une réponse active des moteurs. En effet, au lieu de laisser décélérer le moteur tout seul au moment de couper les gaz (avec l’inertie des hélices le temps est plus ou moins long), l’ESC va faire en sorte de contrer cette inertie et réduire considérablement la vitesse de décélération.
- Motor Timing : Permet de régler le degré d’impulsion des moteurs.
La valeur “Low” correspondant à “0°” ce qui veut dire que l’impulsion se fera lorsque la bobine sera en face de l’aimant. La valeur “High” correspondant à “30°”, l’impulsion sera donc plus tardive. (MediumLow = 8° ; Medium = 15° ; MediumHigh = 23°)
Le timing dépend des moteurs utilisés, il faudra donc faire des essais si vous rencontrez des problèmes de desynchronisation des moteurs (trous à l’accélération).
La valeur “Medium” par défaut correspond à la plupart des moteurs classiques.
- Motor Direction : Un des avantages de passer au firmware BlHeli est qu’il est possible de choisir dans quel sens l’ESC fera tourner son moteur.
Plus besoin d’inverser 2 des trois fils au moment de souder les fils entre l’ESC et le moteur.
Il suffit de mettre “Normal” sur 2 ESC et “Reversed” sur les 2 autres.
Accéder au paramètres
Mode defaut Autre choix
Valeur Réglage Valeur/Réglage Valeur→Réglage Initialisation 0 248 248 120 248 120 248 RPM 248 Type de batterie 120 Lipo 0→NiMH 128 Type de batterie 2 128 Lipo vide→NiMH Low Voltage Limiter 120 réduite 0→Stop 248 Protection de batterie 248 3.0V 120→2.8V 120→3.2V Protection de batterie 2 248 3.0V 248→2.8V Vide→3.2V 128 Motor Direction 128 Normal 120→Inversé Motor Timing 0 Auto 0→7-22 120→22-30 0 Auto Vide→7-22 Vide→22-30 248 Start 120 Soft 128→ACC 0→Very Soft Start 2 Vide Soft 128→ACC Vide 120 Frein 0 Off 120→on Fin de configuration 248 128 248 0
Choix des paramètres alternateur brushless
Avant de commencer à concevoir quelque chose, vous devez connaître le régime nécessaire, le couple nécessaire, la tension de fonctionnement, les ampères max.
$P=C\cdot \omega$ donc $C=\dfrac{P}{\omega}$ et comme $\omega=\dfrac{\pi \cdot N}{30}$ alors $C=\dfrac{30\cdot P}{\pi \cdot N}$
$f[hz] = nombre~de~poles (aimants~nr.)\times RPM / 120$ Exemple: un moteur a 10 aimants et 7000 tr / min alors f = 10 × 7000/120 = 583Hz.
Au vue des paramètres précédents nous montrons le moteur en configuration étoile (λ).
sélection des aimants
La force des aimants est classée en grades: N35, N45, N50, N52 sont très courants, tandis que N52 est le plus fort. J'ai l'impression que les fournisseurs ne sont pas très précis avec leurs spécifications. Les valeurs absolues sont difficiles à mesurer (cela dépend également de la taille de l'aimant), vous ne pouvez donc pas vérifier si les vendeurs exagèrent. Ils ne savent probablement même pas ce qu'ils vendent, mais comme le prix est si bas, vous ne pouvez pas vous plaindre. De plus, la variation entre les «mêmes» aimants peut être énorme +/- 20%.
Mesurer les forces magnétiques des aimants :
Il est important de mesurer les forces magnétiques des aimants les uns par rapport aux autres. Cela permet de sélectionner les plus forts, de manière simple :

Dans le dessins ci-contre il suffit de positionner un morceau de métal ferrique, puis de mesurer la valeur relative.
Équilibrez les aimants:
Une configuration similaire peut être utilisée pour mesurer et comparer leurs masse relative. C'est plus important, car un rotor déséquilibré peut générer de grandes forces vibratoires, et il fait un bruit horrible. La barre peut être réutilisée afin d'éloigner l'aimant des composants magnétiques de la balance. La balance est tarée sans l'aimant, puis l'aimant est placé sur la barre.
Les aimants seront ensuite placés avec les masses les plus proches en oppositions sur le diamètre.
$F= \dfrac{B^2\cdot S}{2\cdot \mu_0}$
avec :
F : la force (Newton)
B : intensité du champ magnétique (Tesla)
S : Surface de l’aimant néodyme (m²)
μ0 : perméabilité du vide
Qualité des aimants néodyme
GRADE T° max
°C Rémanence
Br Intensité du
Champ coercitif Produit énergétique bHc iHc (intrasèque) (BxH)max Gauss (kg) Tesla (mT) kOe kA/m kOe kA/m MGOe kJ/m³ N30 ≤80 10,800-11,200 1008-1012 9.8-10.5 780-836 ≥12 ≥955 28-30 223-239 N33 ≤80 11,400-11,700 1014-1017 10.3-11 820-876 ≥12 ≥955 31-33 247-263 N35 ≤80 11,700-12,100 1017-1021 10.8-11.5 860-915 ≥12 ≥955 33-35 263-279 N38 ≤80 12,200-12,600 1022-1026 10.8-11.5 860-915 ≥12 ≥955 36-38 287-303 N40 ≤80 12,600-12,900 1026-1029 10.5-12.0 860-955 ≥12 ≥955 38-40 303-318 N42 ≤80 12,900-13,200 1029-1032 10.8-12.0 860-955 ≥12 ≥955 40-42 318-334 N45 ≤80 13,200-13,700 1032-1037 10.8-12.5 860-995 ≥12 ≥955 43-45 342-358 N48 ≤80 13,700-14,200 1037-1042 10.8-12.5 860-995 ≥12 ≥955 45-48 358-382 N50 ≤80 14,000-14,600 1040-1046 10.8-12.5 860-995 ≥12 ≥955 47-51 374-406 N52 ≤65 14,200-14,700 1042-1007 10.8-12.5 860-995 ≥12 ≥955 48-53 380-422
Le système magnétique peut être amélioré grace à l'effet du réseau de Halbach

Le fait de mettre des aimants intermédiaires, permet de concentrer le flux et d'eviter la dissipation du flux magnétique.
L'élément essentiel : l'hélice de l'hydrolienne
L'hélice d'une hydrolienne est constituée d'un axe central appelé moyeu, autour duquel sont fixées au minimum deux pales.
Le profil des pales est un élément important qui différencie les différentes hélices, et qui leur donne une fonction précise : pour les avions, on parle d'hélice motrice car celle-ci transfère de l'énergie vers un fluide. Dans le cas d'une hydrolienne, c'est une hélice réceptrice qui à l'inverse récupère de l'énergie grâce au fluide.
Lors de la fabrication de l'hydrolienne, plusieurs critères doivent êtres étudiés au niveau des pales, pour que celles-ci offrent un rendement optimal :
- La longueur des pales, qui doit être assez élevée pour obtenir la puissance voulue
- La largeur des pales, qui contrairement à ce que l'on peut penser, ne doit pas être trop grande pour permettre une plus grande vitesse de rotation de l'hélice, et aussi par un souci de légèreté
- Le nombre de pales, qui varie pour actuellement de 2 à 6 (Sabella "D03" et "D10"). Une hélice bipale permet une vitesse de rotation plus élevée, un poids moins lourd et un coût moins important. Tout comme les hélices de bateaux, l'inconvénient d'avoir seulement deux pales se situe au niveau des vibrations beaucoup plus importantes, les rendant plus fragiles.
- Le profil des pales, qui consiste à vriller les pales afin de ne pas créer un "mur" lors du contact de l'eau contre celles-ci. Malgré tout, plus le vrillage est important, moins la force exercée par l'eau sur les pales sera élevée, et le rendement en subira les conséquences. La difficulté reste donc de trouver un juste milieu.
- La composition des pales, qui doivent être fabriquées avec un matériau très résistant à ce que l'on appelle la fatigue mécanique : c'est un processus qui, sous l'action d'une contrainte (ici l'action des courants), a pour conséquences de déformer voire de fissurer et modifier la structure de ce matériau. De plus, le matériau utilisé doit être suffisamment résistant à l'érosion (accentuée sous l'action de l'eau salée), et avoir l'avantage d'être assez léger. Aujourd'hui, les seuls matériaux répondants à ces contraintes sont les matériaux composites comme la fibre de verre ou la fibre de carbone, recouvert d'un produit antirouille étudié pour résister à l'eau salée
Ainsi, la difficulté rencontrée par un ingénieur chargé de concevoir une hélice d'hydrolienne, est de trouver le bon compromis entre solidité, poids, prix et performances, et ceci en faisant varier les différentes caractéristiques d'une hélice.

Tout comme le vent pour les éoliennes, les courants marins exercent une force (notée F) sur les pales. Cette force se décompose en deux forces : la trainée (notée T) qui est négligeable ici puisqu’elle n’influe pas sur la mise en mouvement de l’hélice ; et la portance (notée P) qui est la cause de la rotation.
Le mouvement de l’eau se matérialise par des lignes de courant, ensembles ont les appelles tubes de courant. On considère que ces tubes ont une certaine section, et que le courant marin possède une certaine vitesse. Lorsqu’un tube du courant rencontre une pale d’hydrolienne une partie du tube peut s’étaler dans la partie creuse alors que l’autre se resserre sur la partie bombée.
Quand elle passe sur la partie bombée les lignes de courant se rapprochent et la section du tube diminue. Cela provoque une augmentation de la vitesse du courant, mais également une baisse de la pression (loi de Bernoulli).
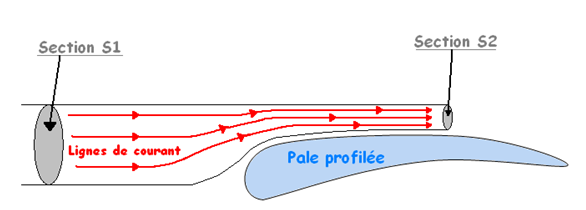
Cette dépression provoque une aspiration de la pale et la met donc en mouvement, c’est ce phénomène que l’on appelle portance. La vitesse de rotation de l’hélice est d’autant plus grande que la vitesse du courant l’est. L’équation de continuité explique ce phénomène, Le fluide (ici l’eau) étant incompressible, la quantité qui pénètre dans un volume donné est à tout instant égale à celle qui en sort, donc dans la section 1 la surface, S1, et plus grande que la surface, S2, de la section2.Pour respecter L’équation de continuité la vitesse de la section 2, V2 est plus important que celle de la section 1, V1.
$S_1\cdot V_1=S_2\cdot V_2$

Pour qu’une hydrolienne se mette en rotation il faut que la vitesse du courant soit s’au-moins de 2ms-1. Plus la vitesse du courant sera rapide plus la vitesse de rotation du rotor sera élevée, et donc plus l’hydrolienne sera rentable.
Un grand nombre de facteur rentre en compte pour un rendement maximum des hydroliennes. Par exemple les hydroliennes construites par l’entreprise « Sabella » ont un rendement égal à vingt-cinq pour cent de la puissance cinétique du fluide (de l’eau)
$P_{cinetique}=\dfrac{1}{2}\rho \cdot S \cdot V^3$
Cette équation met en avant les éléments les plus importants à prendre en compte dans la fabrication et l’implantation des hydroliennes. La masse volumique de l’eau de mer est quasiment constante elle n’a donc pas une importance majeur. Plus la surface de l’hélice « S » (c'est-à-dire son diamètre) est importante meilleur sera le rendement. La vitesse « V » étant élevée au cube « V3 » c'est donc elle qui est primordiale pour obtenir un bon rendement. La vitesse du courant est donc stratégique pour l’implantation d’une hydrolienne.
Profil hydrodynamique
Le paramètrage :

- L= Force de portance perpendiculaire au déplacement du fluide exprimée en newtons (Lift en anglais)
- D= Force de trainée resistante paralelle au déplacement du fluide exprimée en newtons(Drag en anglais)
- α=Angle d'attaque (ou d'incidences géométrique)
- A= Bord d'attaque
- c =Longueur de la corde de référence
- B= Bord de fuite
- d =Position de la cambrure maximale du profil
- AB= Corde de référence du profil
- f =Cambrure maximale
- AMB =Extrados
- r =Rayon du bord d'attaque
- ANB =Intrados
- APB =Ligne de cambrure du profil par rapport à la vitesse de l' écoulement, V∞
- τ =Angle du bord de fuite
- Le milieu des segments perpendiculaires à la corde de référence, tel MN, est appelé squelette du profil ou ligne de cambrure moyenne.
- On note f la plus grande ordonnée de la ligne de cambrure moyenne par rapport à AB.
- Le rapport f/c est dit cambrure relative
- la valeur maximale du segment MN représente l'épaisseur maximale du profil,e max
- L' expression: e max/c = t correspond à l'épaisseur relative maximale. Les profils classiques ont une épaisseur relative de 6 à 20 % située environ à c/3 la cambrure relative est de l' ordre de 6 à 8 % et d/e max varie de 15 à 50%.
- Sur la même figure apparaissent les forces aérodynamiques : L (la portance) et D (la traînée).
Champ électromagnétique
Loi de Faraday : $e=\dfrac{d\phi}{dt}$
- $e$ Force électromotrice
- $\phi$ Flux du champ magnétique subi par la bobine
- $t$ temps
ω=πN/30
ω=2 π f =2 π T
60.T=N
0,2s →
5 tours/min → 5/60=0,083333 tr/s
- le nombre d'encoches
- le nombre de bobines
- le pas des bobines
- les connexions (liaisons entre bobines)
- les interconnexions (liaisons entre sections de bobines)
Couple moteur et ESC
ESC (Electronic Speed Controller)
Les batteries
Batterie NiMh
Elle est composé de plusieurs éléments de 1.2V.
de 1 à 4Ah.
Batterie LiPo
Les batteries Lithium Polymère. Elle est composé de plusieurs cellules de 3,7V.
Le nombre de S est le nombre de cellules, 1S 3,7V, 2S 7,4V, 3S 11,1V,4S 14,8V
La capacité donée en Ah, soit le nombre d'ampère durant une heure Exemple utilisé une batterie : 5Ah.
La capacité de décharge instantannée C, exemple 40 à 50C soit 40x5=200A et 50x5=250A (très peu de temps 10 à 15s).
La capacité de charge, entre 1 et 5C, si elle à 5C on peut la charger en 5x5=25A.
Il y a quelquefois des fils supplémentataires de façon à équilibrer la charge.
Lors de la charge utiliser un sac à lithium.
Si il y a surcharge d'une batterie lipo, il y a risque d'exploision.
Batterie lithium fer phosphate
LFP couramment appelé simplement accumulateur LiFe.
Elles supportent des intensités élevées ce qui leur permet à la fois de fournir beaucoup de puissance et d'être rechargées rapidement.
Les batteries au lithium fer phosphate () sont les plus sûres parmi les batteries au lithium-ion traditionnelles. La tension nominale d'une cellule LFP est de 3,2 V (au plomb : 2 V/cellule). Une batterie LFP de 12,8 V est composée de 4 cellules connectées en série.
Calcul du couple des moteurs
| Couple | en kg.cm | Nombre de KV | en kV à vide |
|---|---|---|---|
| Vitesse | en tr.min-1 | Tension | en V |
| Diamètre de roue | en mm | ||
Fabriquer un moteur Brushless
Commençons par le moteur parfait, sans pertes, η=1
|
| Un rotor est constitué d’un cylindre en fer doux (perméable au champ magnétique) de longueur l dans lequel on a fait des encoches, ici trois (mais il peut y en avoir un nombre quelconque, trois et douze étant très courants en modélisme). On place des bobines en fil de cuivre autour des parties saillantes appelées pôles. On ne considère que la longueur des conducteurs éctiligne, le long des pôles. | |
|---|---|---|
| Ici, un rotor à P = 4 pôles et des bobines à n = 3 spires, ce qui est équivalent à utiliser 4x3x2 = 24 conducteurs rectilignes de longueur L. |
En mécanique le couple s'exprime : $C=F\cdot R$
En électricité :(1) $C=I\cdot k\cdot B \cdot 2 \cdot P\cdot n \cdot L \cdot R$
La vitesse mécanqiue : $\omega=\dfrac{\pi \times N}{30}=\dfrac{V}{R}$
En électricité :(2) $\omega=\dfrac{E}{k\cdot B \cdot 2 \cdot P\cdot n \cdot L \cdot R}$
$R$ étant le rayon du rotor en m,$L$ la longueur du conducteur en m, $F$ la force en Newton, $C$ en Nm,
$E$ la tension en Volt, $I$ courant constant en ampère
$B$ l'induction magnétique en Tesla
$P$ le nombre de pôles et à $n$ le nombre de spires par pôles.
Le coefficient $k$ permet de tenir compte du fait que périodiquement et à tour de rôle chaque bobine est déconnectée et n’agit donc plus, mais également prendre en compte les diverses façons de câbler les bobines entre elles.
(1) $F=I \cdot B\cdot L$ avec (2) $E=F \cdot B\cdot L$ avec
Le pas polaire
On définit le pas polaire du moteur, comme étant le nombre d’encoches sous un pôle.| $P$ le nombre de pôles | Nombre d'encoches | ||
|---|---|---|---|
Sections des fil émaillé
| Diamètre | Masse liéïque | Section mm² | 2 fils parallèles |
3 fils parallèles | |
| Centième | mm | gr/m | |||
| 10 | 0,10 | 0,070 | 0,008 | 0,016 | 0,024 |
| 12 | 0,12 | 0,101 | 0,011 | 0,023 | 0,034 |
| 14 | 0,14 | 0,137 | 0,015 | 0,031 | 0,046 |
| 16 | 0,16 | 0,179 | 0,020 | 0,040 | 0,060 |
| 18 | 0,18 | 0,226 | 0,025 | 0,051 | 0,076 |
| 20 | 0,20 | 0,279 | 0,031 | 0,063 | 0,094 |
| 22.4 | 0,22 | 0,350 | 0,039 | 0,079 | 0,118 |
| 25 | 0,25 | 0,436 | 0,049 | 0,098 | 0,147 |
| 28 | 0,28 | 0,547 | 0,062 | 0,123 | 0,185 |
| 30 | 0,30 | 0,628 | 0,071 | 0,141 | 0,212 |
| 35.5 | 0,36 | 0,880 | 0,099 | 0,198 | 0,297 |
| 40 | 0,40 | 1,117 | 0,126 | 0,251 | 0,377 |
| 45 | 0,45 | 1,414 | 0,159 | 0,318 | 0,477 |
| 50 | 0,50 | 1,746 | 0,196 | 0,393 | 0,589 |
| 56 | 0,56 | 2,190 | 0,246 | 0,493 | 0,739 |
| 63 | 0,63 | 2,771 | 0,312 | 0,623 | 0,935 |
| 65 | 0,65 | 2,950 | 0,332 | 0,664 | 0,995 |
| 67 | 0,67 | 3,134 | 0,353 | 0,705 | 1,058 |
| 71 | 0,71 | 3,520 | 0,396 | 0,792 | 1,188 |
| 75 | 0,75 | 3,927 | 0,442 | 0,884 | 1,325 |
| 80 | 0,80 | 4,469 | 0,503 | 1,005 | 1,508 |
| 85 | 0,85 | 5,045 | 0,567 | 1,135 | 1,702 |
| 90 | 0,90 | 5,656 | 0,636 | 1,272 | 1,909 |
| 95 | 0,95 | 6,301 | 0,709 | 1,418 | 2,126 |
| 100 | 1,00 | 6,982 | 0,785 | 1,571 | 2,356 |
| 106 | 1,06 | 7,845 | 0,882 | 1,765 | 2,647 |
| 112 | 1,12 | 8,758 | 0,985 | 1,970 | 2,956 |
| 118 | 1,18 | 9,722 | 1,094 | 2,187 | 3,281 |
| 120 | 1,20 | 10,054 | 1,131 | 2,262 | 3,393 |
| 125 | 1,25 | 10,910 | 1,227 | 2,454 | 3,682 |
| 130 | 1,30 | 11,800 | 1,327 | 2,655 | 3,982 |
| 140 | 1,40 | 13,685 | 1,539 | 3,079 | 4,618 |
| 150 | 1,50 | 15,710 | 1,767 | 3,534 | 5,301 |
| 160 | 1,60 | 17,874 | 2,011 | 4,021 | 6,032 |
| 170 | 1,70 | 20,179 | 2,270 | 4,540 | 6,809 |
| 180 | 1,80 | 22,622 | 2,545 | 5,089 | 7,634 |
Le nombre de pôles P agit donc ni plus ni moins que comme un réducteur électromagnétique.
Les valeurs classiques de P sont données dans le tableau 4 avec en vis-à-vis les régimes de rotation correspondants maximaux en général admis pour les moteurs « brushless ».
Représentation d'une Bobine dans le stator
Diamètre du fils
| Matériau | Résistivité ρ x 10-8 Ωm | Matériau | Résistivité ρ x 10-8 Ωm | |
|---|---|---|---|---|
| argent | 1,6 | platine | 10 | |
| cuivre | 1,7 | fer | 10 | |
| or | 2,4 | silicium | 10 | |
| aluminium | 2,7 | étain | 18 | |
| magnésium | 4,6 | plomb | 21 | |
| tungstène | 5,6 | germanium | 46 | |
| zinc | 6 | constantan | 49 | |
| nickel | 7 | mercure | 96 | |
| laiton | 7 | nichrome | 100 | |
| cadmium | 7,6 | carbone | 3500 |
Calcul de la résistance électrique d'un fil
| Choisir la matière : | 1.7 x 10-8 Ωm²/m | ||
| Choisir le diamètre en Centième: | 0.1 mm soit 0.008 mm2 | ||
| Longueur : | m | ||
| Résistivité 43.290 Ω, Masse 1.396 gr | |||
Couplage des moteurs en étoile et triangle.
Un moteur avec enroulements en triangle (Δ) donne un faible couple à basse vitesse, mais permet des vitesse de pointe plus élevée.La configuration étoile (λ) donne un couple élevé à bas régime, mais des vitesse de pointe plus faible.

| Connexion | Tension phase U_phase | Courant phase I_phase | Couple max |
|---|---|---|---|
| Star (Y) | U_line / √3 | I_line 0.577 × Δ | |
| Delta (Δ) | U_line | I_line / √3 | 1.732 × Y |
Nombre de bobines, nombre de pôles, nombre d'encoches
Avec une bobine on peut donc faire 2 pôles et pour faire plusieurs pôles (chiffre pairs) il faut donc plusieurs bobines. Dans un bobinage de stator il devra y avoir logiquement autant de bobines que de paires de pôles. Ainsi pour 2 pôles il y aura 1 bobine, pour 4 pôles il y aura 2 bobines, pour 6 pôles 3 bobines, ect…Chaque bobine occupe 2 encoches et il faut donc le double d'encoches que du nombre de bobines. Ce nombre est aussi à multiplier par le nombre de phases pour lequel le moteur va pouvoir être branché : monophasé (1phase), biphasé (2 phases), triphasé (3phases).
Les stators sont donc conçus avec un nombre d'encoches compatible avec le nombre de phase et de pôles.
Le nombre standard d'encoches dans les stators est : 6, 12, 18, 24, 36, 48, 72, pour les plus courantes
Nombre spéciaux : 30, 32, 42, 60
| Nombre d'encoches | Nombre d'encoches par phase | Nombre de pôle P |
|---|---|---|
| 6 | 1 | 2 |
| 12 | 1 | 4 |
| 12 | 2 | 2 |
| 18 | 1 | 6 |
| 18 | 2 | 3 |
| 18 | 3 | 2 |
| 24 | 1 | 8 |
| 24 | 2 | 4 |
| 24 | 4 | 2 |
| 36 | 1 | 12 |
| 36 | 2 | 6 |
| 36 | 3 | 4 |
| 36 | 4 | 3 |
| 36 | 6 | 2 |
| 48 | 1 | 16 |
| 48 | 2 | 8 |
| 48 | 4 | 4 |
| 48 | 8 | 2 |
| 72 | 1 | 24 |
| 72 | 2 | 12 |
| 72 | 3 | 8 |
| 72 | 4 | 6 |
| 72 | 6 | 4 |
| 72 | 8 | 3 |
| 72 | 12 | 2 |
Suivant le nombre d'encoches attribué par pôle, la bobine peut se constituer de plusieurs sections, chaque section occupant plusieurs encoches. Dans un stator les bobines sont logées dans des encoches. Sur un schéma de bobinage on représente le stator déroulé à plat.
Dans sa partie supérieure, un schéma de bobinage renseigne sur:
Flux magnétique
Faisons un calcul « à la louche » :La tension induite est donnée par la loi de Faraday :
V = N. ΔΦ/Δt.
Φ est le flux magnétique : le produit du champ magnétique par la surface.
ΔΦ est la variation du flux dans le temps Δt.
N est le nombre de spires qui entourent le flux.
Prenons un aimant au néodyme dont le champ est 1 tesla et de surface 1 cm².
Le flux qui traverse sa surface est 10^-4 weber.
Si vous faites passer une bobine de 10 tours et de 1 cm² de section devant l’aimant, en 0,1 secondes, la tension induite sera :
10*10^-4/0,1 = 0,01 volts.
Données physiques des aimants
N52 : Br=14200-14700 Gauss ou 1.42-1.47 TeslaLa densité du flux magnétique s'appelle également induction magnétique ou champ B. L'unité de l'induction magnétique est le tesla (unité SI) ou le gauss (10 000 Gauss = 1 Tesla).
Formule pour la densité de flux parallélépipède magnétique
$B=\dfrac{B_r}{\pi}\biggl[ arctan\biggl(\dfrac{L\cdot W}{2\cdot z \sqrt{4z^2+L^2+W^2}}\biggr)-arctan\biggl(\dfrac{L\cdot W}{2(D+z)\sqrt{4(D+z)^2+L^2+W^2}} \biggr)\biggr]$
$B_r$ : Champ rémanent, indépendant de la géométrie de l'aimant (voir Données physiques de l'aimant)
$z$ : Distance de la surface du pôle sur l'axe de symétrie
$L$ : Longueur du parallélépipède
$W$ : Largeur du parallélépipède
$D$ : Epaisseur (ou hauteur) du parallélépipède
L'unité de longueur peut être choisie librement, mais à condition qu'elle soit la même pour toutes les longueurs.
Exemple pour un aimant de N52 40x10x4 nous prendrons
$\Phi=$0,291Wb à 0,301Wb, à 1mm de distance $\Phi$=0,249Wb à 0,258Wb
Formules diverses
$U = -N\cdot \dfrac{\Delta(B\cdot A)}{\Delta t}$$N$ nombre de spires
$B$ champe magnétique des aimants
$A$ section d'une bobine de cuivre $A=\pi (R^2-r^2)$
$E=\dfrac{1}{2}\cdot L \cdot i^2$
- E : l'énergie en Joule (J)
- L : l'inductance de la bobine en Henry toujours (H)
- i : l'intensité du courant parcourant la bobine, en Ampères (A)
une bobine de longueur l, qui possède N spires de surface de section S :
$L=\mu \cdot \dfrac{N^2}{l}\cdot S$
- L : inductance de la bobine en Henry (H)
- N : nombre de spires de la bobine
- l : longueur de la bobine (et non pas du fil qui la compose) en mètres (m)
- S : section de la bobine (de son fil, ici) en mètres carrés (m²)
- μ : perméabilité magnétique du milieu autour duquel sont enroulées les spires
Pour le vide (ou pour l'air "sec"), ce paramètre s'appelle $μ_0$ et est égal à $4\cdot 10^{−7}~H\cdot m^{−1}$.
Unité Henry/m ou newton par ampère carré ($N\cdot A^{−2}$).
Cobalt $\mu_r=250~H\cdot m^{−1}$
Fer $\mu_r=5 000~H\cdot m^{−1}$
Mu-métal $\mu_r=100 000~H\cdot m^{−1}$
Nickel $\mu_r=600~H\cdot m^{−1}$
Paramètres moteur Brushless:
Kv= RPM/Volt.
- Rm= resistance moteur en Ohms.
- Io= Courant sans charge.
N= Kv(I – Io) en RPM
Q= Kq(I – Io) en Nm
η= (V- I Rm)(I - Io)/(V I)
V et I tension et courant en travail.
Imax= sqrt(V Io/Rm)
Qmax= Kq (Imax – Io)
RPMmax= Kv( V – Imax Rm)
ESC
Paramètres utiles existants :- Low Voltage Limiter : permet de définir une tension de coupure des moteurs.
Si vous mettez 3.2V/cell l’ESC va couper l’alimentation si la tension des cellules de la lipo descend sous les 3.2V (9.6V au total). Peut causer une chute du drône si vous ne surveillez pas cette tension.
Il est conseillé de mettre la valeur à Off. - Temperature Protection : Laisser à “Off” car il me semble que nos ESC ZTW ne possèdent pas de capteurs thermiques.
- PWM Frequency/Damped : Sélectionner la valeur Damped Light.
Cette fonction permet une réponse active des moteurs. En effet, au lieu de laisser décélérer le moteur tout seul au moment de couper les gaz (avec l’inertie des hélices le temps est plus ou moins long), l’ESC va faire en sorte de contrer cette inertie et réduire considérablement la vitesse de décélération. - Motor Timing : Permet de régler le degré d’impulsion des moteurs.
La valeur “Low” correspondant à “0°” ce qui veut dire que l’impulsion se fera lorsque la bobine sera en face de l’aimant. La valeur “High” correspondant à “30°”, l’impulsion sera donc plus tardive. (MediumLow = 8° ; Medium = 15° ; MediumHigh = 23°)
Le timing dépend des moteurs utilisés, il faudra donc faire des essais si vous rencontrez des problèmes de desynchronisation des moteurs (trous à l’accélération).
La valeur “Medium” par défaut correspond à la plupart des moteurs classiques. - Motor Direction : Un des avantages de passer au firmware BlHeli est qu’il est possible de choisir dans quel sens l’ESC fera tourner son moteur.
Plus besoin d’inverser 2 des trois fils au moment de souder les fils entre l’ESC et le moteur.
Il suffit de mettre “Normal” sur 2 ESC et “Reversed” sur les 2 autres.
Accéder au paramètres
| Mode | defaut | Autre choix | |
| Valeur | Réglage | Valeur/Réglage | Valeur→Réglage |
| Initialisation | 0 | ||
| 248 | |||
| 248 | |||
| 120 | |||
| 248 | |||
| 120 | |||
| 248 | |||
| RPM | 248 | ||
| Type de batterie | 120 | Lipo | 0→NiMH |
| 128 | |||
| Type de batterie 2 | 128 | Lipo | vide→NiMH |
| Low Voltage Limiter | 120 | réduite | 0→Stop |
| 248 | |||
| Protection de batterie | 248 | 3.0V | 120→2.8V 120→3.2V |
| Protection de batterie 2 | 248 | 3.0V | 248→2.8V Vide→3.2V |
| 128 | |||
| Motor Direction | 128 | Normal | 120→Inversé |
| Motor Timing | 0 | Auto | 0→7-22 120→22-30 |
| 0 | Auto | Vide→7-22 Vide→22-30 | |
| 248 | |||
| Start | 120 | Soft | 128→ACC 0→Very Soft |
| Start 2 | Vide | Soft | 128→ACC Vide |
| 120 | |||
| Frein | 0 | Off | 120→on |
| Fin de configuration | 248 | ||
| 128 | |||
| 248 | |||
| 0 | |||
Choix des paramètres alternateur brushless
Avant de commencer à concevoir quelque chose, vous devez connaître le régime nécessaire, le couple nécessaire, la tension de fonctionnement, les ampères max.$P=C\cdot \omega$ donc $C=\dfrac{P}{\omega}$ et comme $\omega=\dfrac{\pi \cdot N}{30}$ alors $C=\dfrac{30\cdot P}{\pi \cdot N}$
$f[hz] = nombre~de~poles (aimants~nr.)\times RPM / 120$ Exemple: un moteur a 10 aimants et 7000 tr / min alors f = 10 × 7000/120 = 583Hz.
Au vue des paramètres précédents nous montrons le moteur en configuration étoile (λ).
sélection des aimants
La force des aimants est classée en grades: N35, N45, N50, N52 sont très courants, tandis que N52 est le plus fort. J'ai l'impression que les fournisseurs ne sont pas très précis avec leurs spécifications. Les valeurs absolues sont difficiles à mesurer (cela dépend également de la taille de l'aimant), vous ne pouvez donc pas vérifier si les vendeurs exagèrent. Ils ne savent probablement même pas ce qu'ils vendent, mais comme le prix est si bas, vous ne pouvez pas vous plaindre. De plus, la variation entre les «mêmes» aimants peut être énorme +/- 20%.Mesurer les forces magnétiques des aimants :
Il est important de mesurer les forces magnétiques des aimants les uns par rapport aux autres. Cela permet de sélectionner les plus forts, de manière simple :Dans le dessins ci-contre il suffit de positionner un morceau de métal ferrique, puis de mesurer la valeur relative.
Équilibrez les aimants:
Une configuration similaire peut être utilisée pour mesurer et comparer leurs masse relative. C'est plus important, car un rotor déséquilibré peut générer de grandes forces vibratoires, et il fait un bruit horrible. La barre peut être réutilisée afin d'éloigner l'aimant des composants magnétiques de la balance. La balance est tarée sans l'aimant, puis l'aimant est placé sur la barre.Les aimants seront ensuite placés avec les masses les plus proches en oppositions sur le diamètre.
$F= \dfrac{B^2\cdot S}{2\cdot \mu_0}$
avec :
F : la force (Newton)
B : intensité du champ magnétique (Tesla)
S : Surface de l’aimant néodyme (m²)
μ0 : perméabilité du vide
Qualité des aimants néodyme
| GRADE | T° max °C | Rémanence Br | Intensité du Champ coercitif | Produit énergétique | |||||
|---|---|---|---|---|---|---|---|---|---|
| bHc | iHc (intrasèque) | (BxH)max | |||||||
| Gauss (kg) | Tesla (mT) | kOe | kA/m | kOe | kA/m | MGOe | kJ/m³ | ||
| N30 | ≤80 | 10,800-11,200 | 1008-1012 | 9.8-10.5 | 780-836 | ≥12 | ≥955 | 28-30 | 223-239 |
| N33 | ≤80 | 11,400-11,700 | 1014-1017 | 10.3-11 | 820-876 | ≥12 | ≥955 | 31-33 | 247-263 |
| N35 | ≤80 | 11,700-12,100 | 1017-1021 | 10.8-11.5 | 860-915 | ≥12 | ≥955 | 33-35 | 263-279 |
| N38 | ≤80 | 12,200-12,600 | 1022-1026 | 10.8-11.5 | 860-915 | ≥12 | ≥955 | 36-38 | 287-303 |
| N40 | ≤80 | 12,600-12,900 | 1026-1029 | 10.5-12.0 | 860-955 | ≥12 | ≥955 | 38-40 | 303-318 |
| N42 | ≤80 | 12,900-13,200 | 1029-1032 | 10.8-12.0 | 860-955 | ≥12 | ≥955 | 40-42 | 318-334 |
| N45 | ≤80 | 13,200-13,700 | 1032-1037 | 10.8-12.5 | 860-995 | ≥12 | ≥955 | 43-45 | 342-358 |
| N48 | ≤80 | 13,700-14,200 | 1037-1042 | 10.8-12.5 | 860-995 | ≥12 | ≥955 | 45-48 | 358-382 |
| N50 | ≤80 | 14,000-14,600 | 1040-1046 | 10.8-12.5 | 860-995 | ≥12 | ≥955 | 47-51 | 374-406 |
| N52 | ≤65 | 14,200-14,700 | 1042-1007 | 10.8-12.5 | 860-995 | ≥12 | ≥955 | 48-53 | 380-422 |
Le système magnétique peut être amélioré grace à l'effet du réseau de Halbach
Le fait de mettre des aimants intermédiaires, permet de concentrer le flux et d'eviter la dissipation du flux magnétique.
L'élément essentiel : l'hélice de l'hydrolienne
L'hélice d'une hydrolienne est constituée d'un axe central appelé moyeu, autour duquel sont fixées au minimum deux pales.Le profil des pales est un élément important qui différencie les différentes hélices, et qui leur donne une fonction précise : pour les avions, on parle d'hélice motrice car celle-ci transfère de l'énergie vers un fluide. Dans le cas d'une hydrolienne, c'est une hélice réceptrice qui à l'inverse récupère de l'énergie grâce au fluide.
Lors de la fabrication de l'hydrolienne, plusieurs critères doivent êtres étudiés au niveau des pales, pour que celles-ci offrent un rendement optimal :
- La longueur des pales, qui doit être assez élevée pour obtenir la puissance voulue
- La largeur des pales, qui contrairement à ce que l'on peut penser, ne doit pas être trop grande pour permettre une plus grande vitesse de rotation de l'hélice, et aussi par un souci de légèreté
- Le nombre de pales, qui varie pour actuellement de 2 à 6 (Sabella "D03" et "D10"). Une hélice bipale permet une vitesse de rotation plus élevée, un poids moins lourd et un coût moins important. Tout comme les hélices de bateaux, l'inconvénient d'avoir seulement deux pales se situe au niveau des vibrations beaucoup plus importantes, les rendant plus fragiles.
- Le profil des pales, qui consiste à vriller les pales afin de ne pas créer un "mur" lors du contact de l'eau contre celles-ci. Malgré tout, plus le vrillage est important, moins la force exercée par l'eau sur les pales sera élevée, et le rendement en subira les conséquences. La difficulté reste donc de trouver un juste milieu.
- La composition des pales, qui doivent être fabriquées avec un matériau très résistant à ce que l'on appelle la fatigue mécanique : c'est un processus qui, sous l'action d'une contrainte (ici l'action des courants), a pour conséquences de déformer voire de fissurer et modifier la structure de ce matériau. De plus, le matériau utilisé doit être suffisamment résistant à l'érosion (accentuée sous l'action de l'eau salée), et avoir l'avantage d'être assez léger. Aujourd'hui, les seuls matériaux répondants à ces contraintes sont les matériaux composites comme la fibre de verre ou la fibre de carbone, recouvert d'un produit antirouille étudié pour résister à l'eau salée
Ainsi, la difficulté rencontrée par un ingénieur chargé de concevoir une hélice d'hydrolienne, est de trouver le bon compromis entre solidité, poids, prix et performances, et ceci en faisant varier les différentes caractéristiques d'une hélice.
Tout comme le vent pour les éoliennes, les courants marins exercent une force (notée F) sur les pales. Cette force se décompose en deux forces : la trainée (notée T) qui est négligeable ici puisqu’elle n’influe pas sur la mise en mouvement de l’hélice ; et la portance (notée P) qui est la cause de la rotation.
Le mouvement de l’eau se matérialise par des lignes de courant, ensembles ont les appelles tubes de courant. On considère que ces tubes ont une certaine section, et que le courant marin possède une certaine vitesse. Lorsqu’un tube du courant rencontre une pale d’hydrolienne une partie du tube peut s’étaler dans la partie creuse alors que l’autre se resserre sur la partie bombée.
Quand elle passe sur la partie bombée les lignes de courant se rapprochent et la section du tube diminue. Cela provoque une augmentation de la vitesse du courant, mais également une baisse de la pression (loi de Bernoulli).
Cette dépression provoque une aspiration de la pale et la met donc en mouvement, c’est ce phénomène que l’on appelle portance. La vitesse de rotation de l’hélice est d’autant plus grande que la vitesse du courant l’est. L’équation de continuité explique ce phénomène, Le fluide (ici l’eau) étant incompressible, la quantité qui pénètre dans un volume donné est à tout instant égale à celle qui en sort, donc dans la section 1 la surface, S1, et plus grande que la surface, S2, de la section2.Pour respecter L’équation de continuité la vitesse de la section 2, V2 est plus important que celle de la section 1, V1. $S_1\cdot V_1=S_2\cdot V_2$
Pour qu’une hydrolienne se mette en rotation il faut que la vitesse du courant soit s’au-moins de 2ms-1. Plus la vitesse du courant sera rapide plus la vitesse de rotation du rotor sera élevée, et donc plus l’hydrolienne sera rentable.
Un grand nombre de facteur rentre en compte pour un rendement maximum des hydroliennes. Par exemple les hydroliennes construites par l’entreprise « Sabella » ont un rendement égal à vingt-cinq pour cent de la puissance cinétique du fluide (de l’eau)
$P_{cinetique}=\dfrac{1}{2}\rho \cdot S \cdot V^3$
Cette équation met en avant les éléments les plus importants à prendre en compte dans la fabrication et l’implantation des hydroliennes. La masse volumique de l’eau de mer est quasiment constante elle n’a donc pas une importance majeur. Plus la surface de l’hélice « S » (c'est-à-dire son diamètre) est importante meilleur sera le rendement. La vitesse « V » étant élevée au cube « V3 » c'est donc elle qui est primordiale pour obtenir un bon rendement. La vitesse du courant est donc stratégique pour l’implantation d’une hydrolienne.
Profil hydrodynamique
Le paramètrage :- L= Force de portance perpendiculaire au déplacement du fluide exprimée en newtons (Lift en anglais)
- D= Force de trainée resistante paralelle au déplacement du fluide exprimée en newtons(Drag en anglais)
- α=Angle d'attaque (ou d'incidences géométrique)
- A= Bord d'attaque
- c =Longueur de la corde de référence
- B= Bord de fuite
- d =Position de la cambrure maximale du profil
- AB= Corde de référence du profil
- f =Cambrure maximale
- AMB =Extrados
- r =Rayon du bord d'attaque
- ANB =Intrados
- APB =Ligne de cambrure du profil par rapport à la vitesse de l' écoulement, V∞
- τ =Angle du bord de fuite
- Le milieu des segments perpendiculaires à la corde de référence, tel MN, est appelé squelette du profil ou ligne de cambrure moyenne.
- On note f la plus grande ordonnée de la ligne de cambrure moyenne par rapport à AB.
- Le rapport f/c est dit cambrure relative
- la valeur maximale du segment MN représente l'épaisseur maximale du profil,e max
- L' expression: e max/c = t correspond à l'épaisseur relative maximale. Les profils classiques ont une épaisseur relative de 6 à 20 % située environ à c/3 la cambrure relative est de l' ordre de 6 à 8 % et d/e max varie de 15 à 50%.
- Sur la même figure apparaissent les forces aérodynamiques : L (la portance) et D (la traînée).
- $e$ Force électromotrice
- $\phi$ Flux du champ magnétique subi par la bobine
- $t$ temps
Champ électromagnétique
Loi de Faraday : $e=\dfrac{d\phi}{dt}$ω=πN/30
ω=2 π f =2 π T
60.T=N
0,2s →
5 tours/min → 5/60=0,083333 tr/s
Moteur DC
Moteur courant continu (Direct Current)
Conversion d'énergie électrique continue, en énergie mécanique.
Caractéristique de ces moteur
Ce sont des moteurs à courant continu (CC ou DC pour direct current). Imaginons une machine électrique alimentée par une source de tension U, constante. Lorsque le moteur tourne à vide (il ne fait pas d'effort) il n'y a pas besoin de fournir de couple, I est très faible et U, ≈ E.La vitesse de rotation est proportionnelle à U.
Le pont en H
Pour faire tourner un moteur DC dans un sens, il suffit de l'alimenter + à une broche et - à l'autre, pour inverser le sens, il y a juste à inverser la polarité.Pour réaliser cette opération automatiquement, il est nécessaire de réaliser un pont en H.

Le pont en H permet la commande de moteur dans les deux sens de rotation, sans modification du montage, seulement en modifiant l'état des commutateurs. Les commutateurs sont actionnés deux par deux pour faire tourner le moteur dans un sens ou dans l'autre. Les paires de relais peuvent avoir des puissances différentes selon que l'utilisation ne requiert pas le même couple dans un sens que dans l'autre.
Driver L298N double pont en H
Le double pont en H
Le L298N est un double pont en H, c'est à dire qu'il permet de faire tourner deux moteurs dans un sens ou dans l'autre.Utilisation avec un arduino, ce qui donne en C:
// connectez les broches du contrôleur de moteur aux broches numériques Arduino
// moteur 1
int enA = 10;
int in1 = 9;
int in2 = 8;
// moteur 2
int enB = 5;
int in3 = 7;
int in4 = 6;
void setup()
{
// définit toutes les broches de commande du moteur sur les sorties
pinMode (enA, OUTPUT);
pinMode (enB, OUTPUT);
pinMode (in1, OUTPUT);
pinMode (in2, OUTPUT);
pinMode (in3, OUTPUT);
pinMode (in4, OUTPUT);
}
void demoOne ()
{
// cette fonction fera tourner les moteurs dans les deux sens à une vitesse fixe
// allumer le moteur A
digitalWrite (in1, HIGH);
digitalWrite (in2, LOW);
// régler la vitesse à 200 hors de la plage possible 0 ~ 255
analogWrite (enA, 200);
// allumer le moteur B
digitalWrite (in3, HIGH);
digitalWrite (in4, LOW);
// régler la vitesse à 200 hors de la plage possible 0 ~ 255
analogWrite (enB, 200);
delay (2000);
// change maintenant les directions du moteur
digitalWrite (in1, LOW);
digitalWrite (in2, HIGH);
digitalWrite (in3, LOW);
digitalWrite (in4, HIGH);
delay (2000);
// éteignez maintenant les moteurs
digitalWrite (in1, LOW);
digitalWrite (in2, LOW);
digitalWrite (in3, LOW);
digitalWrite (in4, LOW);
}
void demoTwo ()
{
// cette fonction fera fonctionner les moteurs sur la plage de vitesses possibles
// notez que la vitesse maximale est déterminée par le moteur lui-même et la tension de service
// les valeurs PWM envoyées par analogWrite () sont des fractions de la vitesse maximale possible
// par votre matériel
// allumer les moteurs
digitalWrite (in1, LOW);
digitalWrite (in2, HIGH);
digitalWrite (in3, LOW);
digitalWrite (in4, HIGH);
// accélère de zéro à la vitesse maximale
for (int i = 0; i <256; i ++)
{
analogWrite (enA, i);
analogWrite (enB, i);
delay (20);
}
// décélère de la vitesse maximale à zéro
for (int i = 255; i> = 0; --i)
{
analogWrite (enA, i);
analogWrite (enB, i);
delay (20);
}
// éteignez maintenant les moteurs
digitalWrite (in1, LOW);
digitalWrite (in2, LOW);
digitalWrite (in3, LOW);
digitalWrite (in4, LOW);
}
void loop()
{
demoOne ();
delay (1000);
demoTwo ();
delay (1000);
}
Utilisation d'un MX1508 comme double pont en H pour deux moteurs
Très bien pour du tout ou rien, avec inversion de sens de marche.
Equipé d'un MOS L298N, module d'entraînement de moteur à courant continu, double pont en H.
Tension d'alimentation du Module 2 V-10 V
Tension d'entrée du Signal 1.8-7 V
Courant de fonctionnement monocanal de 1,5A, le courant de crête jusqu'à 2,5A, faible courant de veille (moins de 0,1μA)
Et enfin ça mini taille : 24,7x21x5mm.
L'inconvénients de ce petit composant c'est qu'il necéssite deux sorties PWM par moteur, pour réguler la vitesse.
La bibliothèque arduino est bien documentée, mais elle n'existe pas en micropython sur RP2040-ZERO
# Librairie MX1508
# Auteur : Samuel Dupré
# (c) sammy76.free.fr
# Date: April 4th, 2022
# Version: 1.0
#Pour deux moteurs uniquement
#Utilisation :
#from mx1508a import MX1508A
#from time import sleep
#CarteMX=MX1508A(9,10,11,12)
#CarteMX.speed(250,-127)
#sleep(5)
#CarteMX.stop()
from machine import Pin,PWM
class MX1508A:
def __init__(self, in1,in2,in3,in4):
self.IN1=in1
self.IN2=in2
self.IN3=in3
self.IN4=in4
self.pwm1=PWM(Pin(self.IN1))
self.pwm2=PWM(Pin(self.IN2))
self.pwm3=PWM(Pin(self.IN3))
self.pwm4=PWM(Pin(self.IN4))
self.pwm1.freq(2000)
self.pwm2.freq(2000)
self.pwm3.freq(2000)
self.pwm4.freq(2000)
def stop(self):
self.pwm1.duty_u16(0) #stop
self.pwm2.duty_u16(0) #stop
self.pwm3.duty_u16(0) #stop
self.pwm4.duty_u16(0) #stop
def speed(self,M1,M2):
"""Vitesse Moteur 1 et 2"""
def map(x, in_min, in_max, out_min, out_max):
return int((x - in_min) * (out_max - out_min) / (in_max - in_min) + out_min)
#print(Npwm1,Npwm2)
pwmV1 = map(abs(M1), 0, 255, 5000, 50000)
if M1>0:
self.pwm1.duty_u16(pwmV1)
self.pwm2.duty_u16(0)
else:
self.pwm2.duty_u16(pwmV1)
self.pwm1.duty_u16(0)
pwmV2 = map(abs(M2), 0, 255, 5000, 50000)
if M2>0:
self.pwm3.duty_u16(pwmV2)
self.pwm4.duty_u16(0)
else:
self.pwm4.duty_u16(pwmV2)
self.pwm3.duty_u16(0)
#print(pwmV1,pwmV2)
def display(self):
print("IN1\tIN2\tIN3\tIN4")
print("%d\t%d\t%d\t%d" % (self.IN1,self.IN2,self.IN3,self.IN4))
print("PWM1\tPWM2\tPWM3\tPWM4")
print("%d\t%d\t%d\t%d" % (self.pwm1.duty_u16(),self.pwm2.duty_u16(),self.pwm3.duty_u16(),self.pwm4.duty_u16()))
Maintenant elle existe....Exemple : Utilisation de moteur DC pour Fred
Utilisation d'un A4988 comme double pont en H
Principe de fonctionnement
Le A4988 est un modules de pilote pas à pas.Cependant, il m'est venu à l'esprit que pourrait-on utiliser ces modules très bon marché, petits et agréables pour entraîner également des moteurs à courant continu? Lorsque deux moteurs sont branchés sur le module A4988 (au lieu de bobines pas à pas), ils peuvent être entraînés en manipulant la séquence de pas.
Avantages d'utiliser A4988 comme double pont en H :
- Pas cher et largement disponible (<1€)
- petit
- 2A, (de nombreux modules ne peuvent pas vraiment faire cela, dépend de la dissipation thermique et des résistances de détection de courant)
- Seulement 3 datalines nécessaires (ou seulement deux)
- petite chute de tension par rapport à de nombreux ponts en H plus anciens
- limite de courant réglable
- Contrôle de vitesse possible sans pwm externe
- Mode veille
- Modes de décroissance contrôlés pour l'inversion de courant de bobine et la protection de croisement.
- Possibilité de faire fonctionner des moteurs à courant continu au-dessus de leur tension nominale et d'en tirer certains avantages
Les inconvénients
- Logique pas si simple
- Dessus pour contrôler la vitesse des moteurs individuels (mais pas impossible)
- Nécessite une alimentation moteur 7.5-8v
Logique
Les pas à pas sont entraînés par la broche de pas d'impulsions step et la direction est modifiée en réglant la broche dir signal haut ou bas.Chaque fois qu'un pas d'impulsion est envoyé (HIGH, LOW), le courant dans l'une des bobines change sa direction.
Etapes en pas entier pour un moteur pas à pas bipolaire donc à deux enroulement :

Un code qui fait le bon nombre de pas dans la bonne direction en fonction de l'état actuel des moteurs.
// object avoidance robot, two DC motors driven by a A4988 module
// speed is set with value of 0-255 but 255 is the slowest speed and 0 the fastest
int dirPin = 2; //Broche Dir du A4988
int stepperPin = 3; //Broche Step du A4988
int en = 5; //Broche EN du A4988
int state = 0;
int oldSpeed = 0;
int rst = 4;
const int trigPin = 7;
const int echoPin = 8;
void setup() {
Serial.begin(9600);
pinMode(dirPin, OUTPUT);
pinMode(stepperPin, OUTPUT);
pinMode(en, OUTPUT); //enable, active low
pinMode(rst, OUTPUT); //rst, active low
digitalWrite(rst, HIGH);
pinMode(trigPin, OUTPUT);
pinMode(echoPin, INPUT);
digitalWrite(en, LOW);
digitalWrite(dirPin, HIGH);
delay(1000);
randomSeed(analogRead(A0));
}
void loop(){ // some simple object avoidance
int view = ultra();
view = min(view,100); //Valeur la plus petit entre view et 100
if (view < 30) //si view<30
{
if (view <15) //si view<15
{
state = motors(1, 100); //backwards recul durant 800ms
delay(800);
}
int way = random(4,6); //hasard gauche droite
while (ultra() < 30)
state = motors(way, 70); //tand que la distance est <30 alors avance
delay(110);
}
view = map(view, 0, 100, 5, 150);
view = 255-view;
state = motors(2, view); //go forward, speed depends on distance ahead
delay(10);
}
int motors(int robot_direction, int robot_speed) // this determines how many steps to what direction ; determine le nombre d'étapes vers quelle direction
{
switch(robot_direction){
case 0:
if(state != robot_direction){
digitalWrite(en, HIGH); //Desative les moteurs
robot_direction = state;
}
break;
case 1:
if(state != robot_direction || oldSpeed != robot_speed){
digitalWrite(rst, LOW);
delayMicroseconds(5);
digitalWrite(rst, HIGH);
analogWrite(en, robot_speed); //
oldSpeed = robot_speed;
step(2);
}
break;
case 2:
if(state != robot_direction || oldSpeed != robot_speed){
digitalWrite(rst, LOW);
delayMicroseconds(5);
digitalWrite(rst, HIGH);
analogWrite(en, robot_speed);
oldSpeed = robot_speed;
//step(false, 2);
}
break;
case 4:
if(state != robot_direction || oldSpeed != robot_speed){
digitalWrite(rst, LOW);
delayMicroseconds(5);
digitalWrite(rst, HIGH);
digitalWrite(en, LOW);
analogWrite(en, robot_speed);
oldSpeed = robot_speed;
step(1);
}
break;
case 5:
if(state != robot_direction || oldSpeed != robot_speed){
digitalWrite(rst, LOW);
delayMicroseconds(5);
digitalWrite(rst, HIGH);
digitalWrite(en, LOW);
analogWrite(en, robot_speed);
oldSpeed = robot_speed;
step(3);
}
break;
}
return(robot_direction);
}
//make some steps
void step(int stepsit){
//digitalWrite(dirPin,dir);
//delay(50);
for(int i=0;i<stepsit;i++){
digitalWrite(stepperPin, HIGH);
delayMicroseconds(800);
digitalWrite(stepperPin, LOW);
delayMicroseconds(800);
}
}
//Capteur ultra-son
int ultra() {
// just get distance:
int result = 0;
unsigned long duree = 0;
unsigned long dist = 0;
for (int i = 0; i<3; i++)
{
digitalWrite(trigPin, LOW);
delayMicroseconds(2);
digitalWrite(trigPin, HIGH);
delayMicroseconds(10);
digitalWrite(trigPin, LOW);
delayMicroseconds(1);
duree = pulseIn(echoPin, HIGH);
dist = dist +(duree/58.2);
delay(10);
}
dist /= 3;
delay(10);
Serial.println(dist);
result = dist;
return(result);
}
Les codeurs incrémentaux
La position relative.
Le codeur de position incrémental signal un changement de position angulaire.
Lorsqu’un codeur incrémental est mis sous tension, il ne rapportera sa position angulaire qu’une fois qu’il disposera d’un point de référence à partir duquel il pourra effectuer des mesures.
Fonctionnement
Un information de position basée sur la détection et le comptage d'une suite de 0 ou 1. Qu'elles soient données sous forme magnétique, optique, inductifs, capacitifs ou simplement avec des balais sur un rotor.Le pas est la distance qui sépare ces 0 et 1, sur une surface réctiligne ou cylindrique, suivant le besoin.
La vitesse de mesure peut-être déterminée par la formule $Vitesse=\dfrac{pas}{periode}$
Position
En ce qui concerne la position, c'est plus délicat, il faut compter en permanence.Pour déterminer cette position relative à une position initiale, qu'il faut initialiser (comme son nom l'indique).
Mais nous devons également connaitre le sens dans lequel nous comptons, faut-il ajouter ou soustraire les pas
Pour cela il nous faut deux capteurs déphasé d’un quart de période (B) cela ne change rien si nous ajoutons des périodes complètes (exemple : B'). L'implantation des leds n'en sera que plus simple.
Lors de la rotation, chaque capteur récéptionne un signal comme ce qui suit, suivant le sens de rotation ou d'avance:
Nous pouvons donc voir le sens de rotation, en effet, ce n'est pas si visible, alors je vais détailler avec l'utilisation d'un compteur
Observons à la loupe les signaux.
| Addition | Soustraction |
|---|---|
| Lors d'un changement d'état de A on vérifie l'état de B, si c'est identique, on ajoute 1 | Si c'est différent, on enlève 1. |
| Rien de plus simple | |
- Dans le sens de départ, quand le signal de A devient visible, B est visible, et quand il devient invisible, B est invisible.
- Dans l'autre sens, quand le signal de A devient visible, B est invisible, et quand il devient invisible, B est visible.
Comme nous venons de le voir, un simple interruption sur un microcontrolleur!
Un petit exemple sur arduino
volatile int compteur = 0;
volatile int old_compteur=0;
void setup(){
pinMode(2, INPUT); //A
pinMode(3, INPUT); //B
attachInterrupt(0, Int_Calc, CHANGE); //int0 sur P2
Serial.begin(115200);
Serial.println("Start");
}
void loop(){
if (compteur!=old_compteur){
Serial.println(compteur);
}
}
void Int_Calc(){
old_compteur=compteur;
if(digitalRead(2) == digitalRead(3)){
compteur++;
}else{
compteur--;
}
}
En micropython sur ESP8266
from machine import Pin
# declare les broches
SA = Pin(13, Pin.IN)
SB= Pin(12, Pin.IN)
# variable pour l'indication de la position
compteur_position = 0
old_position=0
def fonction_interruptionSA(irq1):
global compteur_position
print(SA.value(),SB.value())
if SB.value() == SA.value():
compteur_position += 1
else:
compteur_position -= 1
# declaration de l'interruption SA (sur front tous le front, sans PULL_UP interne):
SA.irq(trigger=3, handler=fonction_interruptionSA)
#Si demi période uniquement sur front montant
#SA.irq(trigger=Pin.IRQ_RISING, handler=fonction_interruptionSA)
while "true":
if compteur_position!=old_position:
print(compteur_position)
old_position=compteur_position
En assembleur sur Attiny85
; ATtiny85 - 20MHz interne
; +-\/-+
; PB5 1|- -|8 Vcc
; PB3 2|- -|7 PB2 T0/Int0 entrée signal A
; entrée signal B PB4 3|- -|6 PB1
; GND 4|- -|5 PB0
; +----+
.equ SGA = PB2 ;Signal A
.equ SGB = PB4 ;Signal B
.def countLL =r2
.def countLH =r3
.def countHL =r4
.def countHH =r5
.def regA =r16
.def zero =r15
.def savereg =r11
.def justone =r12
.cseg
.org 0000
;************************************************
;* Interrupt Vectors *
;************************************************
rjmp main ; Reset Handler
rjmp VECT_INT0; External Interrupt 0
main:
ldi regA,high(RAMEND) ; set up stack pointer
out SPH,regA
ldi regA,low(RAMEND)
out SPL,regA
ldi regA,(1<<CLKPCE) ; enable the clock prescaler
sts CLKPR,regA ; for 4 cycles
clr regA
sts CLKPR,regA ; and div factor to 1
clr zero
ldi regA,1
mov justone,regA
cbi DDRB,SGA
cbi DDRB,SGB
rcall start_count ;init compteur
loop:
BRTC loop
clt
;Traitement du compteur après modification de la valeur
rjmp loop
;****************************************************
;start_count: configure int0
;****************************************************
start_count:
cli
ldi regA,(0<<ISC01) | (1<<ISC00) ;Any logical change on INT0 generates an interrupt request.
out MCUCR,regA
ldi regA,(1<<INTF0) | (0<<PCIE) ; INT0: External Interrupt Request 0 Enable
out GIMSK,regA
clt ;Flag T=0
clr countLL
clr countLH
clr countHL
clr countHH
sei
ret
;****************************************************
; Interruption 0
;****************************************************
VECT_INT0:
set ;Spécifie le changement du flag T=1
in savereg,SREG ;Avant sauvegarde
push regA
clr regA
sbic PINB,SGB ;skip B=0
inc regA
sbic PINB,SGA ;skip A=0
inc regA
SBRC regA,0 ;
rjmp subLL
addLL:
add countLL,justone
adc countLH,zero
adc countHL,zero
adc countHH,zero
rjmp end_int0
subLL:
sub countLL,justone
sbc countLH,zero
sbc countHL,zero
sbc countHH,zero
end_int0:
pop regA
out SREG,savereg
reti
La vitesse
Calcul de la vitesse La vitesse d’un mouvement est la dérivée par rapport au temps de sa position : $v(t)=\dfrac{dx(t)}{dt}$D’un point de vue pratique, on calcule la dérivée d’un signal grâce la distance et au temps entre deux points de mesure de changement d'état.
Un petit exemple sur arduino
volatile int compteur = 0; //Position (en nombre de pas) du codeur
volatile bool flagT=False; //Booléen en cas de changement de position
volatile float vit = 0; // Vitesse (en nombre de pas par seconde) du codeur
volatile unsigned long t = 0; // temps "courant" (en microsecondes)
void setup(){
pinMode(2, INPUT); //A
pinMode(3, INPUT); //B
attachInterrupt(0, Int_Calc, CHANGE); //int0 sur P2
Serial.begin(115200);
Serial.println("Start");
t = micros(); // Initialisation du temps "courant"
}
void loop(){
if (flagT){
//traitement en cas de déplacement ici
Serial.print(compteur);
Serial.print(" ");
Serial.println(vit);
flagT=False;
}
}
void Int_Calc(){
unsigned long dt = micros() - t; // Temps écoulé depuis le dernier front
t += dt;
flagT=True;
if(digitalRead(2) == digitalRead(3)){
compteur++;
}else{
compteur--;
}
if (dt > 0) {
vit = 1e6/dt; // Calcul de la vitesse (ici en pas par seconde)
}
}
Montage
Eclairage avec deux led IR:Soit une alimentation de 3,3V et des leds de 1,2V (30mA maxi), la résistance sera donc de :
$R=\dfrac{3,3V-2\times 1,2V}{0,025}=36\Omega$
Le standard est plutôt 33Ω ce qui représente :
$I=\dfrac{3,3V-2\times 1,2V}{33}=27mA$
L'ensemble du montage avec des photorécepteurs IR
On utilise le fait que les recepteurs inversés vont bloquer la tension lorsqu’ils sont éclairés (on aura donc le maximum correspondant à la pull-up, tandis que non excitée par la lumière IR, une tension plus faible mais clairement visible.).
Régulation PID
Le régulateur PID, appelé aussi correcteur Proportionnel, Intégral, Dérivé est un système de contrôle permettant d’améliorer les performances d'un asservissement, d'un système ou d'un procédé en boucle fermée.La boucle fermée, permet de savoir l'état réel entre la consigne et la commande.
Introduction
L'erreur entre la consigne et la mesure est ici intégrée par rapport au temps et multipliée par une constante qu'il faudra aussi déterminer en fonction du système.Fonctionnement
Je souhaite remplir un maintenir la température d'une pièce à 20°C avec un radiateur équipé un robinet manuel, plus j'ouvre, plus je chauffe, plus je ferme, moins je chauffe.Règle 1 :
Plus ma température est basse, plus j'ouvre pour atteindre mon objectif.L'ouverture est donc proportionnelle à la différence entre la température voulue de 20°c et la vitesse réelle.
$Erreur=T_{consigne}-T_{actuelle}$
Vous êtes à 17°C, vous ouvrez à fond !
Plus vous vous rapprochez de la température, plus vous fermé le robinet.
Une fois que la température de 20°C atteinte, c'est fini.
$Erreur=0$
- Vous laissez le robinet dans sa position.
- La température commence à baisser dût à la taille de la pièce et à sa déperdition thermique.
- Vous recommencez donc à ouvrir le robinet.
- Plus la température s'approche, plus vous baissez.
- Vous recommencez jusqu'a atteindre une température légèrement inférieure à celle que vous avez choisi.
Règle 2 :
Si votre température reste longtemps en dessous de la consigne, vous ouvrez de plus en plus.Vous décidez donc qu'en plus d'ouvrir proportionnellement à l'erreur commise, vous allez mémoriser cette erreur au cours du temps.
Plus l'erreur globale est importante et plus vous ouvrer.
L'erreur globale est donc la somme des erreurs dans le temps, c'est l'intégration $\int_{0}^{t} erreur(t)dt$
- Lorsque vous stabilisez votre température à 19°C, l'erreur globale augmente et vous vous mettez à ouvrir de plus en plus jusqu’à atteindre 20°C... et le dépasser !
- Arrivé à 20°C, l'erreur globale est encore positive, donc vous continuez à ouvrir.
- Au-delà de 20°C, l'erreur est négative et fait donc diminuer d'erreur globale.
- Vous fermez donc le robinet de plus en plus fortement jusqu’à retourner à 20°C.
- A 20°C, vous recommencez, l'erreur est passé en négatif et vous continuez à fermer... ainsi de suite jusqu'à arriver à vous stabiliser à 20°C après de multiples oscillations.
Règle 3 :
Arrivé à 20°C, vous vous dites : " ça y est, j'y suis ! Mais je n'ai pas été très efficace...Ne faudrait-il pas rajouter une troisième règle afin d'être plus performant ? ".
C'est alors que vous décidez d'anticiper bonne ouverture.
- Plus votre ouverture se rapproche de la l'ouverture optimale, plus vous ouvrez le robinet et plus elle s'éloigne de la tempéraure optimale, plus vous ouvrez !
- Ainsi, si vous vous rapprochez rapidement des 20°C, vous fermez rapidement, afin de ne pas dépasser les 20°C. Ainsi, vous réduisez les oscillations et vous vous stabilisez rapidement la température souhaitez !
Mathématiquement
Le contrôle par PID est une méthode de régulation souvent employée pour les asservissements.Vous ne savez pas ce qu'est un asservissement ? Et bien, c'est un système, capable d'atteindre et de maintenir une consigne grâce aux mesures qu'il effectue.
Imaginez vous, par exemple, dans une voiture sur l'autoroute. Vous souhaitez rouler à 130Km/h sans avoir à appuyer sur l'accélérateur.
La commande de vitesse de croisière de votre voiture devra par elle-même maintenir cette vitesse.
À l'approche d'une pente le système "s'aperçoit" que pour une même puissance au niveau du moteur, il n'atteint plus la consigne des 130Km/h et rajoutera un petit coup d'accélération.
Oui mais de combien ? Et combien de temps faudra t-il au système pour se stabiliser autour de la consigne ?
C'est tout le problème de l'asservissement et le contrôle par PID est un moyen de le résoudre !
Le PID est le régulateur le plus utilisé dans l'industrie.
L'idée de cet organe de contrôle est de modifier intentionnellement la valeur de l'erreur qui subsiste entre la consigne et la mesure effectuée.
Par exemple de la cas d'un asservissement en position l'erreur serait : $\epsilon = c(p) - s(p)$
Proportionnel
$Consigne(t)=K_p\cdot \epsilon(t)$Ce qui en Laplace donne : $Consigne(p)=K_p\cdot \epsilon(p)$
Intégral
Au contrôle proportionnel, nous pouvons ajouter l'intégration de l'erreur. Dans ce cas nous obtenonsune régulation PI.$Consigne(t)=K_p\cdot \epsilon(t)+K_i \int \epsilon(\tau) \,d\tau $
Ce qui en Laplace donne : $Consigne(p)=K_p\cdot \epsilon(p)+K_i\dfrac{\epsilon(p)}{p}$
Dérivé
Pour obtenir un contrôle en PID, il nous faut encore rajouter un terme.Celui-ci consiste à dériver l'erreur entre la consigne et la mesure par rapport au temps et a le multiplier lui aussi par une constante. $Consigne(t)=K_p\cdot \epsilon(t)+K_i \int \epsilon(\tau) \,d\tau+K_d\dfrac{d\epsilon(\tau)}{d\tau} $
Ce qui en Laplace donne : $Consigne(p)=K_p\cdot \epsilon(p)+K_i\dfrac{\epsilon(p)}{p}+K_d\cdot p \cdot \epsilon(p)=\epsilon(p)\big[K_p+K_i\dfrac{1}{p}+K_d\cdot p\big]$
Nous avons besoin d'un terme dérivé car le contrôle PI peut amener à un dépassement de la consigne, ce qui n'est pas toujours très souhaitable (exemple d'inversion de polarité dans le cas de moteurs électriques).
Le terme dérivé permet de limiter cela. Lorsque le système s'approche de la consigne, ce terme freine le système en appliquant une action dans le sens opposé et permet ainsi une stabilisation plus rapide.
$Commande=K_p\cdot e(t)+K_i \int e(t) \,dt +K_d \dfrac{d}{dt} e(t)$
$u(t) = K_p e(t) + K_i \int_{0}^{t} e(t)dt + K_d \dfrac{de}{dt}$
Implémentation d'un PID sur un robot
Le PID, ce n'est que cela! Mémoriser l'erreur, faire la somme des erreurs et la différence de l'erreur courante avec l'erreur précédente.Le régulateur proportionnel (P : Règle 1)
La commande de ce régulateur est proportionnelle à l'erreur.$Commande = K_p \cdot Erreur$
$K_p$ est le coefficient de proportionnalité de l'erreur à régler de façon manuelle.
Le régulateur proportionnel intégral (PI : Règle 1 et 2)
La commande de ce régulateur est proportionnelle à l'erreur, mais aussi proportionnelle à l'intégrale de l'erreur.On rajoute donc à la commande généré par le régulateur proportionnel, la somme des erreurs commises au cours du temps.
$Commande=K_p\cdot Erreur+K_i \cdot \sum Erreur$
$K_i$ est le coefficient de proportionnalité de la somme des erreurs. Il faut aussi le régler de façon manuelle.
Le régulateur proportionnel dérivé (PD : Règle 1 et 3)
La commande de ce régulateur est proportionnelle à l'erreur, mais aussi proportionnelle à la dérivée de l'erreur.La dérivée de l'erreur correspond à la variation de l'erreur d'un échantillon à l'autre et se calcule simplement en faisant la différence entre l'erreur courante et l'erreur précédente (c'est une approximation linéaire et locale de la dérivée).
$Commande=K_p\cdot Erreur+K_d \cdot (Erreur - Erreur~précédente)$
$K_d$ est le coefficient de proportionnalité de la variation de l'erreur. Il faut régler ce coefficient manuellement.
Le régulateur proportionnel intégrale dérivé (PID : Règle 1,2 et 3)
Ici, la commande est à la fois proportionnelle à l'erreur, proportionnelle à la somme des erreurs et proportionnelle à la variation de l'erreur.$Commande=K_p\cdot Erreur+K_i \cdot \sum Erreur+K_d \cdot (Erreur - Erreur~précédente)$
Vous devez donc faire une mesure sur votre système pour pouvoir calculer l'erreur et ainsi appliquer le PID.
Cette mesure est à faire régulièrement à une certaine fréquence d'échantillonnage.
Tous les x millisecondes, faire :
erreur = consigne - mesure;
somme_erreurs += erreur;
variation_erreur = erreur - erreur_précédente;
commande = Kp * erreur + Ki * somme_erreurs + Kd * variation_erreur;
erreur_précédente = erreur
Comment régler les coefficients d'un PID ?
Le réglage des coefficients $K_p, K_i$ et $K_d$ d'un PID peut se faire "à la main" par essais/erreurs.Tout d'abord, sachez qu'il ne sert à rien de vouloir régler les trois coefficients en même temps !
Il y a trop combinaisons possibles et trouver un triplet performant relèverait de l'exploit. Il vaut mieux y aller par étape.
- Etape 1 : Mettre en place un simple régulateur proportionnel (les coefficients $K_i$ et $K_d$ sont donc nuls).
- Etape 2 : Le coefficient $K_i$. Celui-là va permettre d'annuler l'erreur finale du système afin que celui-ci respecte exactement la consigne.
- Etape 3 : Le coefficient $K_d$ permet de rendre le système plus stable. Son réglage permet donc de diminuer les oscillations.
Par essais/erreurs, il faut régler le coefficient $K_p$ afin d'améliorer le temps de réponse du système.
C'est-à-dire qu'il faut trouver un $K_p$ qui permette au système de se rapprocher très vite de la consigne tout en faisant attention de garder la stabilité du système : il ne faut pas que le système réponde très vite tout en oscillant beaucoup !
Il faut donc régler $K_i$ pour avoir une réponse exacte en peu de temps tout en essayant de minimiser les oscillations apportées par l'intégrateur !
Le PID parfait n'existe pas, tout est une question de compromis.
Certaines applications autoriseront un dépassement afin d'améliorer le temps de stabilisation, alors que d'autres ne l'autoriseront pas (exemple, contrôler le déplacement d'un outil. S'il y a dépassement dans le PID, l'outil dépassera dimension).
Tout dépend donc du cahier des charges. Chacun des coefficients à un rôle à jouer sur la réponse à une consigne :
- L'erreur statique, c'est l'erreur finale une fois que le système est stabilité. Cette erreur doit être nulle. Pour diminuer l'erreur statique, il faut augmenter $K_p$ et $K_i$.
- Le dépassement, c'est le rapport entre le premier pic et la consigne. Ce dépassement diminue si $K_p$ ou $K_i$ diminuent ou si $K_d$ augmente.
- Le temps de montée correspond au temps qu'il faut pour arriver ou dépasser à la consigne. Le temps de montée diminue si $K_p$ ou $K_i$ augmentent ou si $K_d$ diminue.
- Le temps de stabilisation, c'est le temps qu'il faut pour que le signal commette une erreur inférieure à 5% de la consigne. Ce temps de stabilisation diminue quand $K_p$ et $K_i$ augmentent.
En effet, l'intégrateur fera la somme des erreurs au cours du temps!
Si on échantillonne deux fois plus vite, on sommera deux fois plus d'échantillons. Du coup, le coefficient $K_i$ devra être divisé par 2.
A l'inverse, pour le dérivateur, si on double la fréquence d'échantillonnage, il faudra doubler le coefficient $K_d$ afin de garder les mêmes performances du PID.
Plus la fréquence d'échantillonnage est élevé et plus le PID sera performant. (En effet, plus on échantillonne souvent et plus l'intégration et la dérivée seront précises). Quelques remarques sur les coefficients
Quand on augmente coefficient de proportionnalité $K_p$
- La stabilité augmente
- La rapidité diminue
- La précision diminue
- La stabilité augmente
- La rapidité diminue
- La précision reste parfaite
- La stabilité augmente
- La rapidité augmente
- La précision ne bouge pas
- Si Kp augmente alors la montée sera plus rapide mais il y aura plus de dépassement
- Si Ki augmente alors la montée sera plus rapide et l'erreur statique sera plus faible mais le régime stationnaire sera plus long à atteindre
Exemple en python
Soit un moteur avec un commande entre -1000 et 1000 pour sa vitessePetit exemple de calcul de PID.
Kp=4.
Ki=0.
Kd=0.
encoderval=0
consigne=384*4
commande_max=1000.
commande=1.
erreur_precedente = 0
somme_erreurs=0
while encoderval<>consigne:
encoderval-=(commande/abs(commande))*1 #commande pour la variation
erreur=encoderval-consigne
somme_erreurs += erreur
variation_erreur = erreur - erreur_precedente
commande = (Kp * erreur) + (Ki * somme_erreurs) + (Kd * variation_erreur)
if abs(commande)>1000:
commande=(commande/abs(commande))*1000
print (("commande "+str(commande)+" encoderval "+str(encoderval)))
erreur_precedente = erreur
Méthode Ziegler–Nichols
Dans un premier temps $K_I=0$ et $K_D=0$.On augmente $K_P$ jusqu'à ce que la sortie oscille de manière importante.
Alors on prends $K_U=K_P$ gain maximal (ou gain critique).
On note $T_U$ la période d'oscillation du signal.
| Performances rapides (1/4 du rapport d'amortissement) | |||||
|---|---|---|---|---|---|
| Type de contrôle | $K_P$ | $T_I$ | $T_D$ | $K_I$ | $K_D$ |
| P | $0,5\cdot K_U$ | - | - | - | - |
| PI | $0,45\cdot K_U$ | $0,83\cdot T_U$ | - | $0,54\dfrac{K_U}{T_U}$ | - |
| PD | $0,8\cdot K_U$ | - | $0,125\cdot T_U$ | - | $0,1\cdot K_U\cdot T_U$ |
| PID | $0,6\cdot K_U$ | $0,5\cdot T_U$ | $0,125\cdot T_U$ | $1,2\dfrac{K_U}{T_U}$ | $0,075\cdot K_U\cdot T_U$ |
| Performances normales (du dépassement) | |||||
| P | $0,2\cdot K_U$ | - | - | - | - |
| PI | $0,18\cdot K_U$ | $0,83\cdot T_U$ | - | - | - |
| PID | $0,25\cdot K_U$ | $0,5\cdot T_U$ | $0,125\cdot T_U$ | - | - |
| lentes (peu de dépassement) | |||||
| P | $0,13\cdot K_U$ | - | - | - | - |
| PI | $0,13\cdot K_U$ | $0,83\cdot T_U$ | - | - | - |
| PID | $0,15\cdot K_U$ | $0,5\cdot T_U$ | $0,125\cdot T_U$ | - | - |
| lentes (aucun de dépassement) | |||||
| PID | $0,2\cdot K_U$ | $0,5\cdot T_U$ | $0,33\cdot T_U$ | $0,4\dfrac{K_U}{T_U}$ | $0,066\cdot K_U\cdot T_U$ |
Méthode du Régleur
Le réglage du régulateur se fait par petit pas. Le système fonctionnant en boucle fermée, autour du point de consigne, on observe la réponse de la mesure à un échelon de consigne.En régulation proportionnelle
On cherche la bande proportionnelle correcte en observant la réponse du système à un échelon de consigne- $K_p$ varie
- $K_d=0$
- $K_i=\infty$
En régulation proportionnelle dérivée
On cherche le temps dérivé correct en observant la réponse du système à un échelon de consigne- $K_p$ fixé
- $K_d$ varie
- $K_i=\infty$
En régulation proportionnelle intégrale dérivée
On cherche le temps intégral correct en observant la réponse du système à un échelon de consigne- $K_p$ fixé
- $K_d$ fixé
- $K_i$ varie
- Si $K_d$ amène des instabilités pour de petites valeurs, on préférera prendre $K_d=0$
- L’ordre P→D→I permet un réglage plus fin de l’action D que l’ordre P→I→D.